Предел числовой последовательности. Предел функции в бесконечности и точке. Бесконечно малые величины и их свойства. Бесконечно большие величины. Основные теоремы о пределах: теорема единственности, предел суммы, произведения, частного. Признаки существования предела. Второй замечательный предел. Число e. Понятие о натуральных логарифмах. Непрерывность функции в точке и на промежутке. Основные теоремы о непрерывных функциях. Раскрытие неопределенностей вида 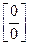 ,
, 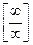 ,
, 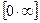 ,
, 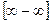 ,
, 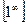 . Вычисление пределов ([1 или 5, § 6.1 – 6.8]; [2 или 6, § 6.1 – 6.3, 6.5], или [3, § 6.1 – 6.10], или [4, §2.1 – 2.10]).
. Вычисление пределов ([1 или 5, § 6.1 – 6.8]; [2 или 6, § 6.1 – 6.3, 6.5], или [3, § 6.1 – 6.10], или [4, §2.1 – 2.10]).
Наряду с понятием функции, понятия предела и непрерывности являются основными в разделе «Введение в анализ».
Понятие предела в учебнике [1, или 5, или 3] рассматривается для числовой последовательности 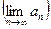 и для функции: в бесконечности
и для функции: в бесконечности 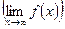 и в точке
и в точке 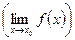 . Для выяснения смысла этих понятий необходимо использовать их геометрическую интерпретацию. Весьма важными являются понятия бесконечно малых и бесконечно больших величин ([1, или 5, или 3, § 6.3, 6.4]), суть которых сводится к тому, что при своем изменении бесконечно малая (по абсолютной величине) будет меньше любого, как угодно малого числа
. Для выяснения смысла этих понятий необходимо использовать их геометрическую интерпретацию. Весьма важными являются понятия бесконечно малых и бесконечно больших величин ([1, или 5, или 3, § 6.3, 6.4]), суть которых сводится к тому, что при своем изменении бесконечно малая (по абсолютной величине) будет меньше любого, как угодно малого числа 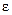 > 0, а бесконечно большая будет больше любого как угодно большого числа М > 0.
> 0, а бесконечно большая будет больше любого как угодно большого числа М > 0.
Нужно знать взаимосвязь бесконечно малых и бесконечно больших величин, свойства бесконечно малых, с помощью которых доказываются теоремы о пределах. Следует обратить внимание на признаки существования пределов, особенно на теорему 1 ([1 или 5, или 3, § 6.5]), часто позволяющую установить наличие предела значительно проще, чем при использовании его определения.
Необходимо (без вывода) знать второй замечательный предел в двух формах записи:
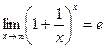 и
и 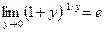 .
.
Понятие непрерывности функции (в точке, на промежутке) является более простым, чем предел, так как оно выражается непрерывностью графика при прохождении данной точки, данного промежутка (без отрыва карандаша от листа бумаги). Наряду с интуитивным представлением надо знать определение непрерывности функции в точке и на промежутке, свойства непрерывных функций, а также то, что всякая элементарная функция непрерывна в каждой точке области определения и может иметь разрыв лишь на границах области определения.
 2015-03-07
2015-03-07 429
429








