Доказательство. i) Докажем теорему для точек прямой (для E1)

i) Докажем теорему для точек прямой (для E¹).

1) Пусть точка C делит отрезок AB в отношении l.

1 случай. x_A < x_B, то есть |AB| = x_B - x_A.

- Если точка C не лежит на луче [AB), то l < 0, x_C < x_A и |AC| = x_A - x_C.

Так как по определению |AC| = |l| |AB|, то x_A - x_C = - l (x_B - x_A), тогда x_C = (1-l)x_A + lx_B.

- Если точка C лежит на луче [AB), то l > 0, x_C ³ x_A и |AC| = x_C - x_A.

Так как по определению |AC| = |l| |AB|, то x_C - x_A = l (x_B - x_A), тогда x_C = (1-l)x_A + lx_B.

2 случай. x_B < x_A, то есть |AB| = x_A - x_B (аналогичен случаю 1)

2) Пусть координаты точек A,B и C таковы, что x_C = (1-l)x_A + lx_B, тогда

x_C - x_A = l (x_B - x_A).

2 случай. x_B < x_A, то есть |AB| = x_A - x_B (аналогичен случаю 1)

Возьмем точку D, которая делит отрезок AB в отношении l. Тогда, как уже доказано, ее координаты подчиняются соотношению x_D = (1-l)x_A + lx_B., то есть x_D =x_C.

Так как декартова система координат устанавливает биективное соответствие между точками прямой и множеством действительных чисел, то из равенства координат точек D и C следует, что они совпадают, то есть точка C делит отрезок AB в отношении l.

ii) Докажем теорему для точек плоскости (для E²).

1 случай. Прямая AB не параллельна ни одной из координатных осей.

Пусть точки A’,B’- проекции точек A и B на координатную ось (Ox),

точки A’’, B’’ проекции точек A и B на координатную ось (Oy).

1) Пусть точка C делит отрезок AB в отношении l, и точки C’,C’’ - проекции точки C на оси (Ox), (Oy) соответственно.

Тогда точка C’ делит отрезок A’B’ (и точка C’’ делит отрезок A’’B’’) в отношении l, поэтому по пункту (i) x_C = (1-l)x_A + lx_B и y_C = (1-l)y_A + ly_B.

2) Пусть точка C такова, что для ее координат 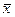_C справедливо равенство

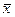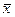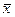_C = (1 - l) _A + l _B.

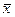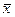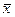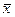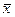Возьмем точку D, которая делит отрезок AB в отношении l. Тогда, как уже доказано, ее координаты подчиняются соотношению _D = (1 - l) _A + l _B, то есть _D = _C.

Так как декартова система координат устанавливает биективное соответствие между точками плоскости и множеством упорядоченных пар действительных чисел, то из равенства координат точек D и C следует, что они совпадают, то есть точка C делит отрезок AB в отношении l.

2 случай. Прямая AB параллельна одной из координатных осей.

Пусть прямая AB параллельна оси (Ox). Тогда для всех точек прямой координаты по оси (Oy) равны между собой, поэтому достаточно доказать теорему для координат точек по оси (Ox). Повторим доказательство 1-го случая, рассматривая только проекции на ось (Ox).

Если прямая AB параллельна оси (Oy), то рассуждения аналогичны.

iii) Докажем теорему для точек пространства (для E³).

Доказательство аналогично представленному в пункте (ii).