2015-04-12
438
Определение: говорят, что квадратичная форма q(x) приводится к главным осям в En, если в En ∃ ОНБ, в котором q(x) имеет канонический вид, то есть q(x)= λ1( 
)2+…+ λn( 
)2, где x=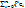 
Теорема: всякая квадратичная форма приводится к главным осям.
Доказательство: пусть q(x)- квадратичная форма на En. Зафиксируем в En некоторый ОНБ [e]: q(x)⇿ 
. То есть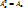 
- симметрично.
Ae – собственный линейный оператор A.
[e]: q(x) ⇿ 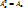⇿ A (так как 
= 
, то A – самосопряженный)
Согласно спектральной теории самосопряженного оператора в En ∃ ОНБ [ẽ]=(ẽ1,…,ẽn) из собственных векторов оператора A, то есть A⇿ 
= 
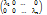
Из леммы следует, что [ẽ]: q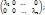(x)⇿ 
= = 
x= 
, то q(x)= λ1( 
)2+…+ λn( 
)2 .
