Парную игру с нулевой суммой удобно исследовать, если функция выигрыша задается платежной матрицей.
Пусть игроки А и В располагают конечным числом возможных действий – чистых стратегий. Обозначим их соответственно А 1, А 2, …, Аm и В 1, В 2, …, Вn. Игрок А может выбрать любую чистую стратегию Аi 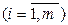 , а игрок В может выбрать любую чистую стратегию Вj
, а игрок В может выбрать любую чистую стратегию Вj 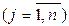
 . Пара стратегий (Аi, Вj) однозначно определяет результат игры aij (aij – выигрыш игрока А или проигрыш игрока В при условии, если игрок A придерживается своей чистой стратегии Ai, а игрок B – чистой стратегии Bj). Если известны значения исхода игры aij для каждой пары (Аi, Вj) чистых стратегий, то можно составить платежную матрицу выигрышей игрока А (проигрышей игрока В) (рисунок 1).
. Пара стратегий (Аi, Вj) однозначно определяет результат игры aij (aij – выигрыш игрока А или проигрыш игрока В при условии, если игрок A придерживается своей чистой стратегии Ai, а игрок B – чистой стратегии Bj). Если известны значения исхода игры aij для каждой пары (Аi, Вj) чистых стратегий, то можно составить платежную матрицу выигрышей игрока А (проигрышей игрока В) (рисунок 1).
| B 1 | … | Bn | a i | |
| A 1 | a 11 | … | a 1 n | a1 |
| … | … | … | … | … |
| Am | am 1 | … | amn | a m |
| b j | b1 | b n |
Рисунок 1. Платежная матрица игры
Решить матричную игру означает определить наилучшую стратегию игрока A, а также наилучшую стратегию игрока B. Если рассматривается стратегическая игра, то предполагается, что противники одинаково разумны, и каждый из них делает все для того, чтобы добиться своей цели.
Используя этот принцип, найдем наилучшую стратегию игрока A. Выбирая стратегию Ai, мы должны рассчитывать, что игрок B ответит на нее той из своих стратегий Bj, для которой выигрыш игрока A будет минимальным. Найдем минимальное число aij в каждой строке матрицы:
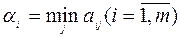 .
.
Эта величина есть гарантированный (самый малый) выигрыш игрока A при выборе им чистой стратегии A i. Значения a i обычно записываются в правом столбце платежной матрицы (см. рисунок 1). Очевидно, что желающий перестраховаться игрок A должен предпочесть другим стратегиям ту, для которой гарантированный выигрыш a i максимален.
Обозначим это максимальное значение 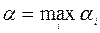 . Величина
. Величина 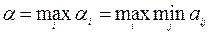 есть гарантированный выигрыш, который игрок A может получить в игре, и называется нижней ценой игры или максимином. Стратегия, обеспечивающая игроку A получение нижней цены игры, называется максиминной стратегией.
есть гарантированный выигрыш, который игрок A может получить в игре, и называется нижней ценой игры или максимином. Стратегия, обеспечивающая игроку A получение нижней цены игры, называется максиминной стратегией.
Аналогичные рассуждения могут быть проведены по поводу действий игрока В. С его точки зрения, в платежной матрице приведены проигрыши. В каждом из столбцов он должен найти максимальное значение проигрыша при выборе стратегии B j:
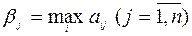 .
.
Значения b j записываются в дополнительной строке платежной матрицы (см. рисунок 1).
Выбирать стратегию игроку B следует так, чтобы минимизировать величину проигрыша при любых действиях соперника, т. е. обеспечить 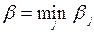 . Величина
. Величина 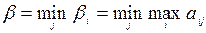 называется верхней ценой игры (минимаксом), а соответствующая ей чистая стратегия Bj – минимаксной.
называется верхней ценой игры (минимаксом), а соответствующая ей чистая стратегия Bj – минимаксной.
Можно показать, что максимин не превосходит минимакс, т. е. a £ b. Если в игре нижняя цена равна верхней (a = b), то говорят, что игра имеет седловую точку и чистую цену игры g = a = b. Пару чистых стратегий (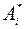 ,
, 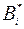 ), соотвествующих g, называют седловой точкой матричной игры, а элемент aij *платежной матрицы, стоящий на пересечении i *-й строки и j *-го столбца, – седловым элементом платежной матрицы. Он одновременно является минимальным в своей строке и максимальным в своем столбце. Стратегии
), соотвествующих g, называют седловой точкой матричной игры, а элемент aij *платежной матрицы, стоящий на пересечении i *-й строки и j *-го столбца, – седловым элементом платежной матрицы. Он одновременно является минимальным в своей строке и максимальным в своем столбце. Стратегии 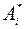 и
и 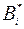 , образующие седловую точку, являются оптимальными. Значения
, образующие седловую точку, являются оптимальными. Значения 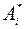 ;
; 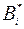 ;g называют решением игры.
;g называют решением игры.
 2015-04-17
2015-04-17 396
396








