Найдем стационарные состояния дискретного спектра частицы в кулоновском поле с потенциальной энергией:
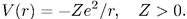 (7.1)
(7.1)
Решение уравнения для радиальной функции 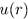 при фиксированном значении I в виде
при фиксированном значении I в виде
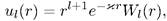 (7.2)
(7.2)
где
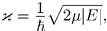 (7.3)
(7.3)
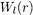 — некоторый полином. Решением соответствующего уравнения для
— некоторый полином. Решением соответствующего уравнения для 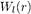 является вырожденная гипергеометрическая функция:
является вырожденная гипергеометрическая функция:
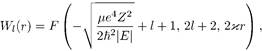 (7.4)
(7.4)
причем квадратичная интегрируемость функции 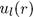 имеет место только в том случае, когда F сводится к полиному конечной степени. Это, в свою очередь, осуществляется тогда и только тогда, когда первый аргумент вырожденной гипергеометрической функции есть целое отрицательное число или нуль:
имеет место только в том случае, когда F сводится к полиному конечной степени. Это, в свою очередь, осуществляется тогда и только тогда, когда первый аргумент вырожденной гипергеометрической функции есть целое отрицательное число или нуль:
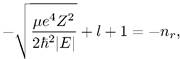 (7.5)
(7.5)
где
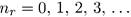 (7.6)
(7.6)
Отсюда получаем энергетический спектр системы:
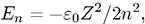 (7.7)
(7.7)
где
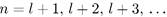 (7.8)
(7.8)
для выбранного значения I. Величина
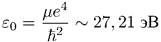
называется атомной единицей энергии. Из (7.8) следует, что если фиксировать не l, а n, то l может принимать следующие значения:
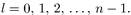 (7.10)
(7.10)
Квантовое число n может принимать только целые положитель-
положительные значения:
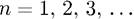 (7.11)
(7.11)
и согласно (7.7) играет роль главного квантового числа. Радиальные функции, соответствующие паре квантовых чисел n, l, имеют вид
|
|
|
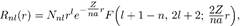 (7.12)
(7.12)
где
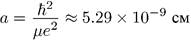 (7.13)
(7.13)
называется атомной единицей длины. Заметим, что вырожденная гипергеометрическая функция в (7.12) сводится к обобщенному полиному Лагерра:
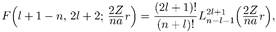 (7.14)
(7.14)
а нормировочный множитель 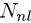 определяется из условия нормировки.
определяется из условия нормировки.
Мы видим, что дискретный энергетический спектр частицы в кулоновском поле (7.7) представляет собой систему уровней, сгущающихся к точке Е = 0, которая дискретному спектру не принадлежит. Энергия каждого стационарного состояния однозначно определяется главным квантовым числом n и не зависит от орбитального квантового числа l.
При данном значении энергии 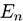 , т.е. при фиксированном значении главного квантового числа n, орбитальное квантовое
, т.е. при фиксированном значении главного квантового числа n, орбитальное квантовое
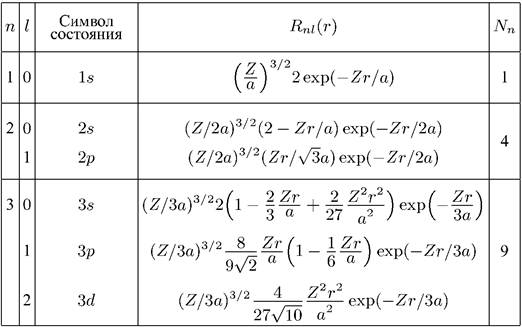
Таблица 1. Низшие стационарные состояния в кулоновском поле
число l принимает n различных значений (7.10), каждому из которых соответствует 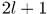 линейно независимых функций
линейно независимых функций
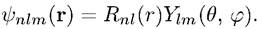
Следовательно, помимо вырождения по магнитному квантовому числу m, обязательного для любого сферически-симметричного поля, в кулоновском поле для всех уровней, кроме основного, имеет место дополнительное вырождение по орбитальному квантовому числу l, которое было названо «случайным».
Нетрудно проверить, что кратность вырождения каждого энергетического уровня есть
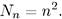 (7.15)
(7.15)
В табл. 1 приведены квантовые числа низших стационарных состояний частицы в кулоновском поле и указана кратность вырождения 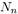 каждого энергетического уровня.
каждого энергетического уровня.
Отметим, что каждому энергетическому уровню, кроме основного, принадлежат состояния как с положительной (l — четное), так и с отрицательной (l — нечетное) четностью.
|
|
|
Рассмотрим линейную комбинацию Ѱ собственных функций, принадлежащих некоторому энергетическому уровню:
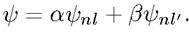
Пусть при этом четности чисел  и
и 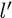 противоположны. Функция Ѱ
противоположны. Функция Ѱ
является собственной функцией, принадлежащей тому же энергетическому уровню, но она не обладает определенной четностью. Поэтому частица, движущаяся в кулоновском поле с некоторым определенным значением энергии, может находиться не только в
состояниях с определенной четностью, но и в таких состояниях, в которых четность не имеет определенного значения (исключением является низший энергетический уровень, которому соответствует только четное состояние). Так, например, в состоянии 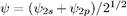 четность не имеет определенного значения.
четность не имеет определенного значения.
Укажем средние значения 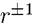 и
и 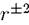 в произвольном стационарном состоянии
в произвольном стационарном состоянии 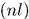 :
:
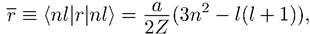 (7.16)
(7.16)
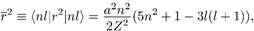 (7.17)
(7.17)
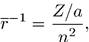 (7.17а)
(7.17а)
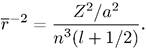 (7.176)
(7.176)
С помощью (7.16) и (7.17) можно найти дисперсию координаты r в произвольном состоянии 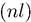 :
:
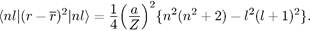 (7.18)
(7.18)
Отсюда видно, что при фиксированном n координата r имеет минимальный разброс, если l имеет максимальное возможное значение 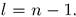 Такие кулоновские орбиты называются «круговыми».
Такие кулоновские орбиты называются «круговыми».
В заключение отметим, что волновые функции (7.12), вычисленные при произвольном Z,называются водородоподобными. При Z = 1 они описывают стационарные состояния атома водорода. Надо помнить, что в этом случае в уравнение Шредингера, а следовательно и в соотношения (7.9) и (7.13), входит не масса электрона, а приведенная масса атома водорода
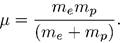
(7.19)
Поскольку 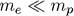 , то возникающая при этом поправка к спектру (7.7) и к волновым функциям (7.12) невелика. Однако иногда ее необходимо учитывать.
, то возникающая при этом поправка к спектру (7.7) и к волновым функциям (7.12) невелика. Однако иногда ее необходимо учитывать.
 2015-04-17
2015-04-17 1738
1738






