Пример

а) Константы 0,1 и функция монотонны. Отрицание немонотонно.

б) Дизъюнкция и конъюнкция любого числа переменных являются монотонными функциями.

в) Функция 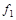(табл.4.11) немонотонна, так как (001)<(101), а 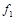(001)> 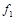(101). Функция 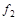(табл.4.11) монотонна.

Таблица 4.11


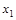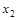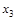
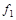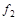
0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1	0 0 1 0 0 1 1 1 1 0 0 1 0 1 1 1

Проверка монотонности функции непосредственно по определению требует анализа таблицы функции и может оказаться довольно громоздким делом. Поэтому, для опознавания монотонности полезна следующая теорема, которая здесь приводится без доказательства.

Теорема. Всякая булева формула, не содержащая отрицаний, представляет монотонную функцию, отличную от 0 и 1. И наоборот: для любой монотонной функции, отличной от 0 и 1, найдется представляющая ее булева формула без отрицаний.

Следствие. Сокращенная ДНФ монотонной функции - единственная тупиковая, а значит, и минимальная ДНФ.

Теорема. Множество всех монотонных функций является замкнутым классом.

Доказательство. Эта теорема непосредственно следует из предыдущей теоремы и того очевидного обстоятельства, что подстановка формул без отрицаний в формулу без отрицаний снова дает формулу без отрицаний. Теорема доказана.

Следствие. Класс монотонных функций является замыканием системы функций .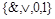

Это утверждение вытекает из того, что всякая булева формула без отрицаний является суперпозицией дизъюнкций и конъюнкций.

Теперь перейдем к основной проблеме этой главы: каковы необходимые и достаточные условия функциональной полноты для произвольной системы функций 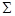? Как уже было показано выше, система 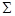полна, если дизъюнкция, конъюнкция и отрицание являются суперпозициями функций из 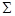. Поэтому, будем искать свойства функций, позволяющие выразить через них булевы операции.

Лемма 1 (о немонотонных функциях). Если функция 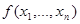немонотонна, то подстановкой констант из нее можно получить отрицание.

Доказательство: Пусть 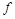немонотонна. Тогда существуют наборы 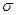и 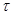, такие, что, 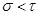, , 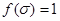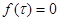. Есл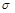и и 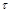отличаются k компонентами, то в этих компонентах в 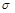стоят нули, а в 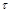единицы. Берем набор и, заменяя эти компоненты по одному единицами, получаем цепочку , в которой любые два набора, стоящие рядом, отличаются только в одной компоненте (такие наборы называются соседними). Ясно, что в такой цепочке найдутся два соседних набора 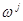, , 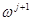таких, что 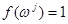, 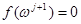. Пусть они отличаются в i -й компоненте, тогда 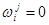, , 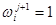остальные их компоненты одинаковы. Подставим эти значения остальных компонент в 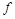. Получим функцию 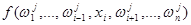от 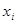, обозначим ее 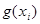. Но 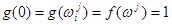; 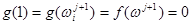. Следовательно, 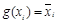. Лемма доказана.

Пример. Функция 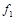, представленная в табл.4.11 немонотонна. Минимизировав данную функцию, получим:

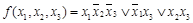Подставив 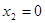, , 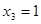получим отрицание:

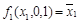Лемма 2 (о нелинейных функциях). Если функция 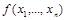нелинейна, то с помощью подстановки констант и использования отрицаний из нее можно получить дизъюнкцию и конъюнкцию.

Доказательство: Пусть 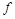нелинейна. Тогда ее полином Жегалкина содержит конъюнкции переменных. Выберем самую короткую из них: 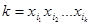. Положим 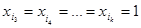, а для всех 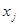, не входящих в 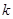, 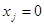. Подстановка этих констант в полином обратит 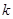в 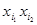, а остальные конъюнкции в 0, и полином функции 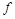примет вид 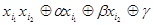, где 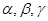- коэффициенты, равные 0 и 1 и зависящие от конкретной функции 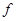. Функции, получающиеся при всех восьми возможных комбинациях значений , приведены в табл. 4.12, в которой, для наглядности, обозначено 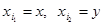, а отрицание в последнем столбце обозначено через 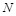. Поскольку каждая из функций , 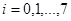- результат подстановки констант в 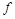, то последний столбец табл.4.12 содержит искомое представление дизъюнкции или конъюнкции в виде суперпозиции отрицаний, констант и исходной функции 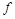. Для перехода от полученного представления к представлению двойственной функции (от конъюнкции к дизъюнкции и наоборот) дополнительно требуется отрицание (по закону де Моргана). Лемма доказана.

Таблица 4.12

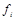
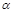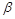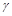
	Вид полинома	Эквивалентная булева функция	Искомая суперпозиция
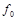
0 0 0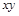
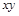
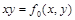
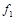
0 0 1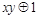
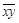
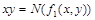
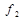
0 1 0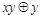
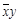
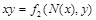
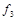
0 1 1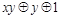
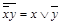
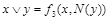
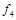
1 0 0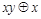
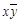
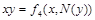
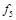
1 0 1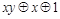
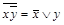
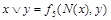
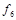
1 1 0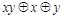
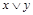
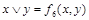
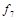
1 1 1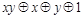

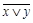
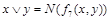
Пример. 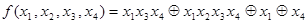. Самая короткая конъюнкция 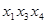. Полагаем 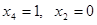. Тогда 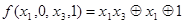, что соответствует 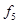в табл.4.12. Отсюда получаем: ;

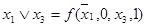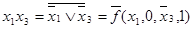
Две доказанные леммы позволяют получить все булевы операции с помощью немонотонных функций, нелинейных функций и констант. Это еще не функциональная полнота в обычном смысле, так как константы с самого начала предполагались данными. Однако, такое предположение оправдано при синтезе логических схем, где системе логических функций соответствует набор типовых логических элементов, а полнота системы означает возможность реализовать с помощью этих элементов любые логические функции. При схемной реализации константы 0 и 1 специальных элементов не требуют. Поэтому, имеет смысл ввести ослабленное понятие функциональной полноты: система функций 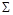называется функционально полной в слабом смысле, если любая логическая функция может быть представлена формулой над системой 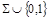, то есть является суперпозицией констант и функций из .

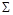Сформулируем первую теорему о функциональной полноте.

Теорема. Для того, чтобы система функций 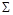была функционально полной в слабом смысле, необходимо и достаточно, чтобы она содержала хотя бы одну немонотонную и хотя бы одну нелинейную функцию.

Необходимость. Классы монотонных и линейных функций замкнуты и содержат 0 и 1. Поэтому, если 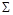не содержит немонотонных или нелинейных функций, то их нельзя получить с помощью суперпозиций функций из 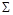и констант.

Достаточность. Пусть 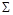содержит немонотонную и нелинейную функцию. Тогда, по лемме 1, подстановкой констант из монотонной функции получаем отрицание, а затем, по лемме 2, из нелинейной функции с помощью отрицаний и констант получаем дизъюнкцию и конъюнкцию. Теорема доказана.

Для формулировки необходимых и достаточных условий сильной полноты рассмотрим еще три замкнутых класса.

Функция 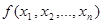называется сохраняющей 0, если 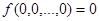. Функция называется сохраняющей 1, если 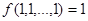. Оба класса функций, сохраняющих 0 и сохраняющих 1, являются замкнутыми, что проверяется подстановкой констант в суперпозицию.

Напомним, что функция называется самодвойственной, если 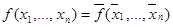. Класс самодвойственных функций замкнут.

Его замкнутость доказывается прямой выкладкой. (Чтобы избежать громоздких обозначений, далее она проводится не в самом общем виде, обобщение очевидно.)

Пусть 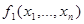, 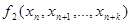- самодвойственные функции. Подставим 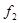в 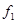вместо 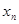. Получим:

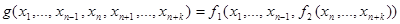Тогда в силу самодвойственност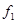и и :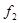

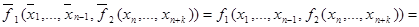
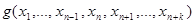
то есть, 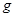является самодвойственной.

Теперь сформулируем вторую - основную теорему о функциональной полноте.

Теорема. Для того, чтобы система функций 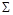была функционально полной (в сильном смысле), необходимо и достаточно, чтобы она содержала: 1) нелинейную функцию, 2) немонотонную функцию, 3) несамодвойственную функцию, 4) функцию, не сохраняющую 0, 5) функцию, не сохраняющую 1.

Необходимость. Необходимость следует из замкнутости пяти классов, упомянутых в условии теоремы.

Достаточность. При доказательстве достаточности отметим следующее. Леммы 1 и 2 используют константы. Поэтому, сначала нужно получить константы (из условий 3-5 теоремы) и только потом можно воспользоваться теоремой о функциональной полноте в слабом смысле (предыдущей теоремой).

Прежде всего отметим, что если 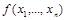несамодвойственна, то подстановкой в нее 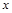и 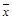можно получить константу. Действительно, ввиду несамодвойственности 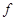найдется набор 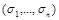, такой, что 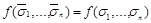. Но тогда функция 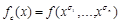является константой, т.к.

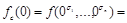
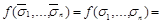
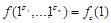
Пусть теперь 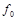не сохраняет 0, 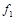не сохраняет 1, 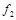несамодвойственна (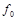, , 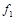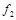не обязательно должны быть различными). Рассмотрим два случая:

1. Если 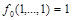, то функция 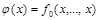есть константа 1, так как 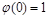по определению 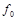и 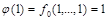, а функция 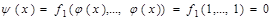, то есть 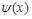есть константа 0.

2. Если же 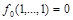, то 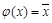, так как по определению 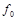и 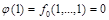. Но тогда, из 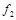подстановко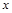й и 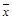получим функцию 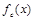, являющуюся константой, а используя еще раз 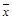, получим вторую константу. Итак, в любом случае выполнение условий 3-5 теоремы достаточно для получения констант 0, 1.