Индекс Лернера

Индекс (коэффициент) Лернера как показатель степени конкурентности рынка позволяет избежать трудностей, связанных с подсчетом нормы до­ходности. Мы знаем, что при условии максимизации прибыли цена и предельные издержки связаны друг с другом посредством эластичности спроса по цене. Монополист назначает цену, превышающую предельные издержки на величину обратно пропорциональную эластичности спроса. Если спрос чрезвычайно эластичен, то цена будет близка к предельным издержкам, и, следовательно, монополизированный рынок будет похож на рынок совершенной конкуренции. Исходя из этого, положения А. Лернер предложил в 1934 году индекс, определяющий монопольную власть:

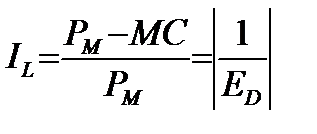(2.11)

где, P_M – цена

MC – издержки

E_D – эластичность спроса

Индекс Лернера принимает значения от нуля (на рынке со­вершенной конкуренции) до единицы (для чистой монополии с нулевы­ми предельными издержками). Чем выше значение индекса, тем выше монопольная власть и дальше рынок от идеального состояния совершен­ной конкуренции.

Сложность вычисления индекса Лернера связана с тем, что информацию о предельных издержках довольно сложно получить. В эмпирических исследованиях часто используется такая формула для определения предельных издержек на основе данных о средних перемен­ных затратах.

Значение индекса Лернера можно прямо связать с показателем кон­центрации продавцов па рынке олигополии, предположив, что он опи­сывается моделью Курно. Для 1-й фирмы на таком рынке предельная выручка составляет:

(2.12)

Помножив второе слагаемое на P/P и Q/Q, получим:

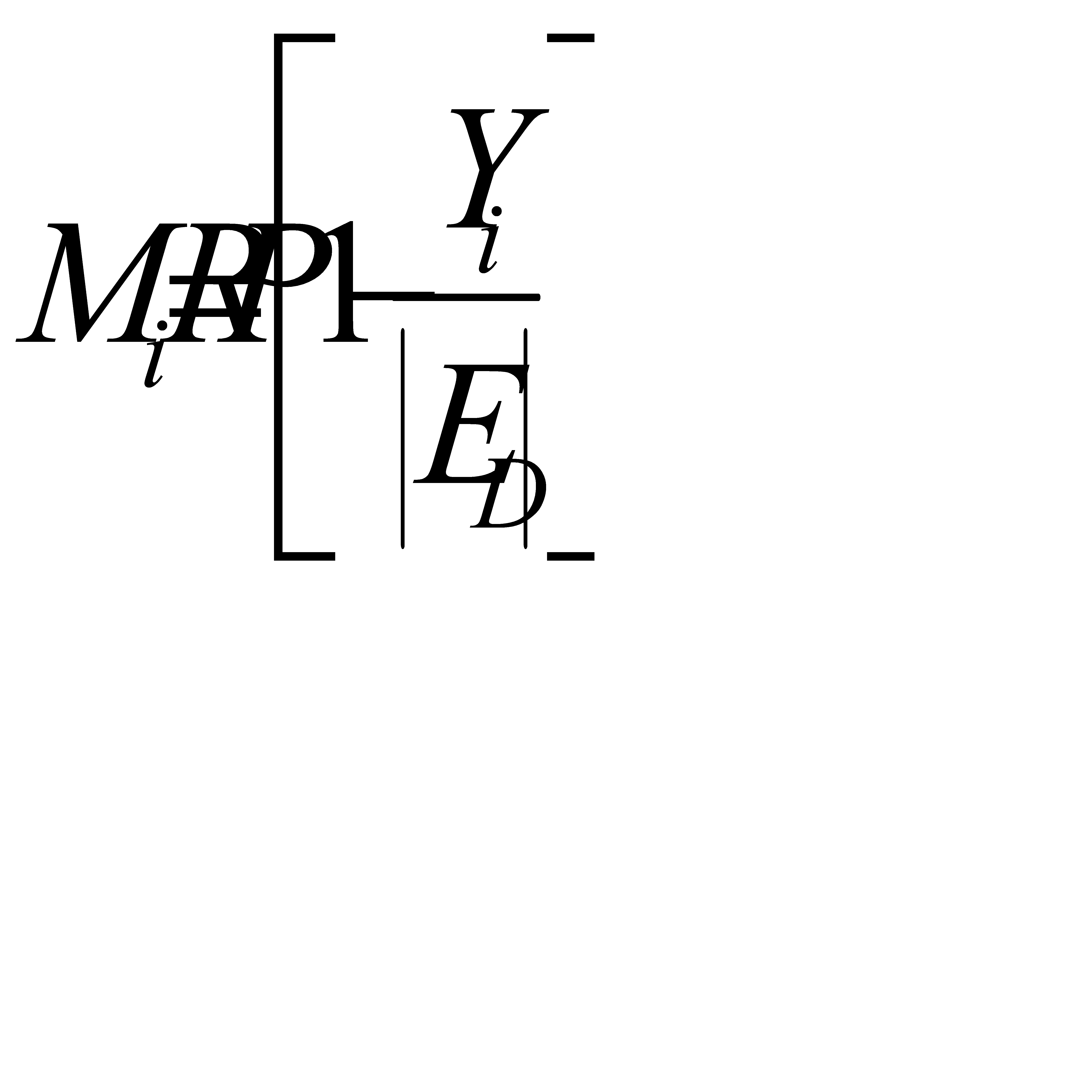(2.13)

где Y_i = q_i \ Q – рыночная доля фирмы.

Таким образом, индекс Лернера будет находиться в прямой зависимости от доли фирмы на рынке и обратной от показателя эластичности спроса по цене.

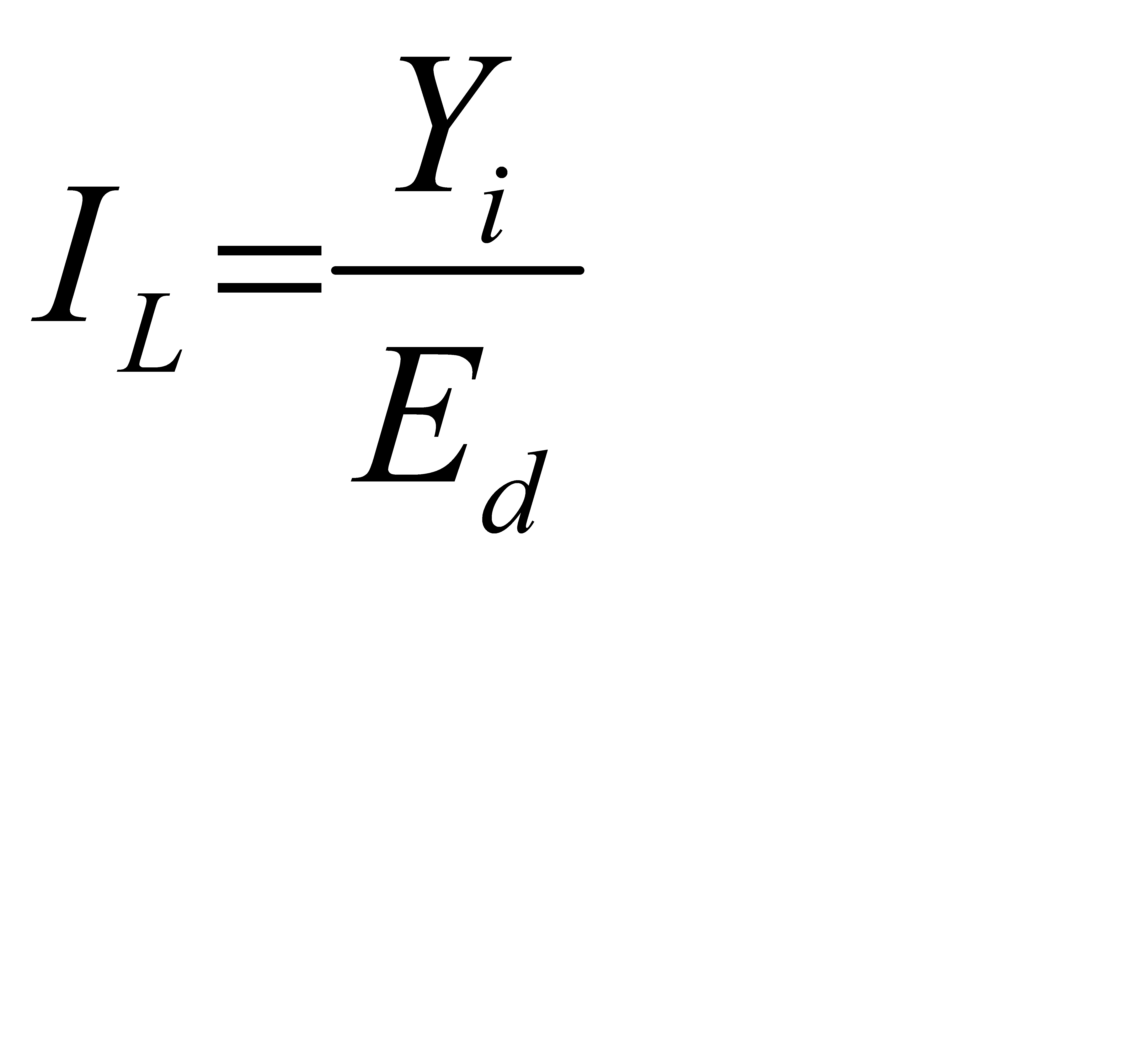(2.14)

Средний для отрасли индекс Лернера будет вычисляться по формуле:

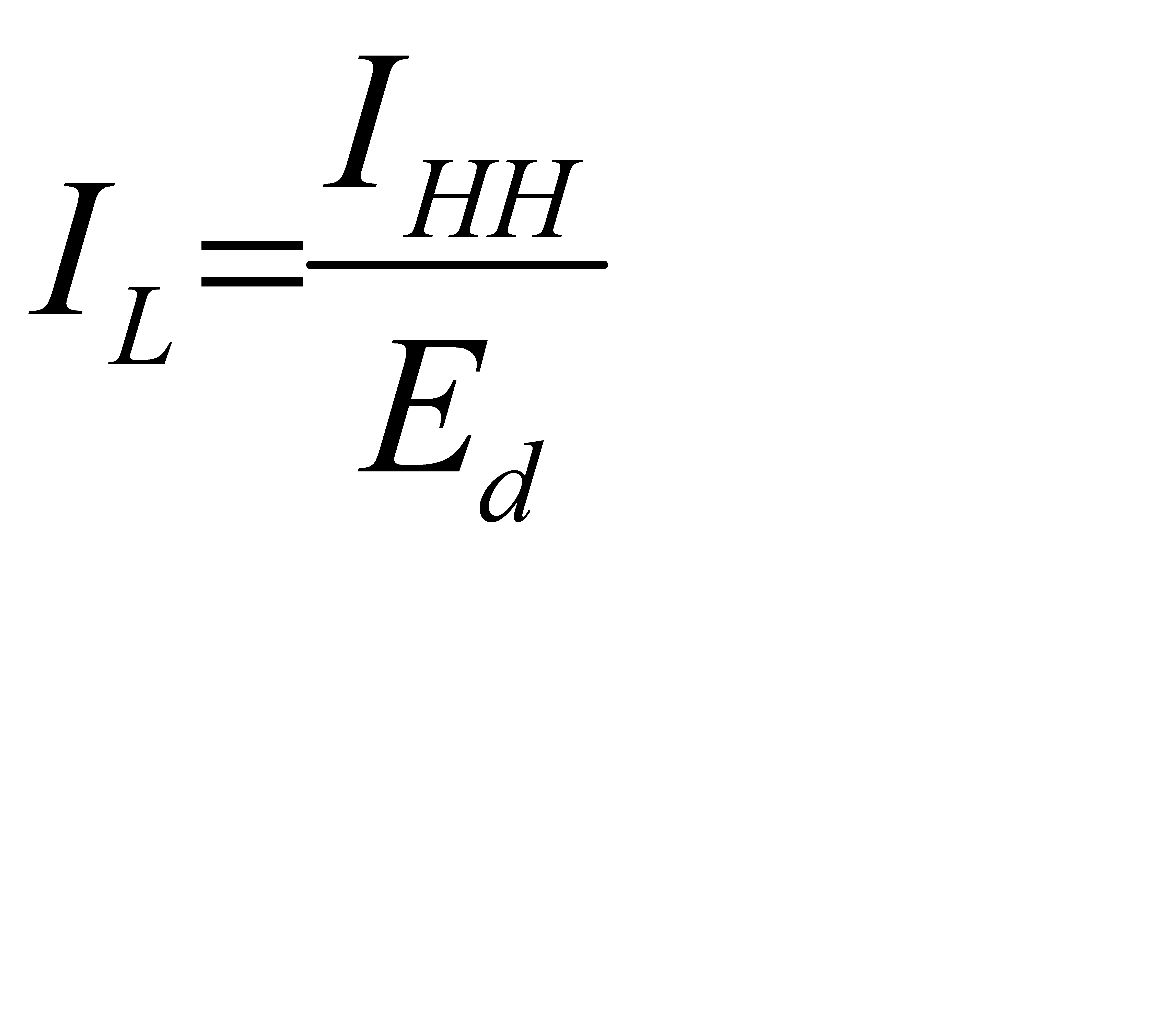(2.15)