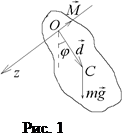
Теоретическое описание. Математическим маятником называется материальная точка, подвешенная на невесомой и нерастяжимой нити

Математическим маятником называется материальная точка, подвешенная на невесомой и нерастяжимой нити. Физическим маятником называется любое твердое тело, способное совершать колебания под действием силы тяжести вокруг неподвижной горизонтальной оси, проходящей через точку О, лежащую выше его центра масс С.

Отклоним маятник из положения равновесия на некоторый угол j (рис.1) и отпустим. Возникает вращающий момент силы тяжести 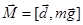, проекция которого на ось z равна 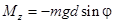, где m – масса тела; d – расстояние от оси вращения z до центра масс С. Знак минус выражает тот факт, что момент M_z стремится уменьшить угол j. При малых колебаниях угол j мал и можно положить 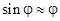, поэтому 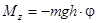. Применяя уравнение динамики вращательного движения 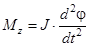, получим дифференциальное уравнение гармонических колебаний физического маятника: 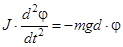или 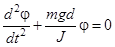. Сравнивая это уравнение с уравнением колебаний материальной точки 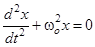можно найти собственную частоту колебаний физического маятника 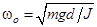или выразить период

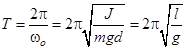, (1)

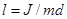где – (2)

приведенная длина физического маятника (длина нити математического маятника с таким же периодом, что и у физического).

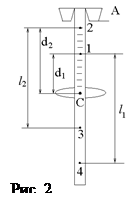В данной работе физический маятник представляет собой металлический стержень, в центре которого жестко закреплен массивный груз (рис.2). На верхней половине стержня находится призма, которую можно перемещать и закреплять в выбранном положении. Экспериментально устанавливается зависимость периода колебаний маятника от расстояния между ребром А призмы и центром масс С. Вид графика приведен на рис.3.

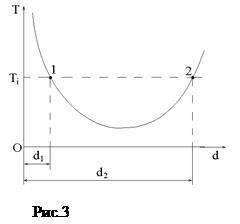Для произвольного значения периода T_i прямая, параллельная оси абсцисс, дает две точки пересечения с кривой: 1 и 2. То есть, располагая ребро призмы в точке 1, находящейся на расстоянии d ₁ от С, а затем в точке 2, находящейся на расстоянии d ₂ от С, получим одинаковые значения периода колебаний маятника: T₁=T₂=T. Тогда на основании (1) и (2) получаем, что приведенная длина l ₁ относительно точки 1 равна приведенной длине l ₂ маятника относительно точки 2.

Используя выражение (2), имеем

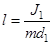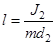, . (3)

По теореме Штейнера

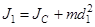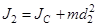и (4)

где 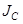– момент инерции относительно горизонтальной оси, проходящей через центр масс С и параллельной оси колебаний маятника.