Введение
Методы решения дифференциальных уравнений условно классифицируются по следующему признаку:
- точное решение, позволяющее представить искомую функцию в элементарных функциях;
- приближенные решения, в которых точное решение получается как предел некоторой последовательности; в этом случае, как правило, используются разложения искомой функции в ряды Тэйлора, Фурье и так далее;
- численные решения, когда искомая функция определяется для конечного числа значений аргумента в узлах разностной сетки.
Благодаря развитию современных средств вычислительной техники методы решения дифференциальных уравнений с использованием компьютеров, в том числе персональных, получили широкое распространение. Задачи теплопроводности, механики жидкостей и газов, механики твердого деформируемого тела и многие другие были решены в основном благодаря широкому использованию сеточных методов. Вместе с тем следует иметь в виду, что неквалифицированное применение разностных схем к решению дифференциальных уравнений приводит к получению решений, далеких от истинных. Поэтому понятен интерес к теории разностных схем, позволяющей еще на стадии разработки алгоритма решения сложной инженерной проблемы выяснить условия успешной реализации вычислительной модели.
|
|
|
Одним из важнейших вопросов является оценка порядка аппроксимации применяемой разностной схемой исходного дифференциального уравнения, позволяющая судить о степени адекватности используемой сеточной модели исходной дифференциальной задаче. Основная идея решения дифференциальных уравнений численными методами на ЭВМ заключается, как правило, в сведении исходной задачи к решению систем алгебраических (линейных или нелинейных) уравнений. При этом естественно возникает вопрос о разрешимости этой получаемой системы. Численное решение сходится к точному, если при неограниченном увеличении числа алгебраических уравнений решение дискретизированной задачи стремится к решению исходной задачи. Поскольку решить систему с бесконечным числом алгебраических уравнений невозможно, весьма актуальным представляется вопрос об оценке погрешности получаемых численных решений исходной дифференциальной задачи.
Обыкновенные дифференциальные уравнения
Решением, интегралом или интегральной кривой обыкновенного дифференциального уравнения первого порядка
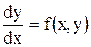 , или
, или 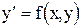
называется дифференцируемая функция y = y(x), удовлетворяющая этому уравнению, то есть такая, что 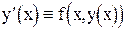 на некотором участке изменения аргумента x.
на некотором участке изменения аргумента x.
Различают три типа задач:
- задача Коши, когда для искомой функции задается условие для одного из значений аргумента, принимаемого за начальное, 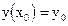 ;
;
|
|
|
- граничная задача[1], когда условия на искомую функцию задаются для нескольких различных значений аргумента, 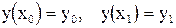 ,
, 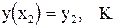 ;
;
- задачи на собственные значения, когда в формулировку задачи входят неопределенные параметры, определяемые из самой задачи (нахождение частот собственных колебаний многомассовых систем).
Численные методы следует применять лишь к корректно поставленным задачам, то есть таким, для которых решение существует, единственно и непрерывно зависит от входных данных, то есть от начальных (граничных) условий и коэффициентов уравнения.
Численное решение задачи считается корректным, если исходная задача поставлена корректно, и ее дискретный аналог сохраняет свойства корректности, то есть получаемая система алгебраических уравнений однозначно разрешима и устойчива [2] по входным данным.
Пример 1.1. На материальную точку массы m, находящуюся на гладкой горизонтальной поверхности, действует горизонтальная периодическая сила 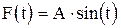 . Определить закон движения точки, если ее начальная скорость v0.
. Определить закон движения точки, если ее начальная скорость v0.
Уравнение, описывающее движение точки, имеет вид:
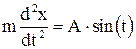 .
.
В качестве начальных условий примем:
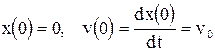 .
.
Интегрирование исходного уравнения с заданными начальными условиями дает решение
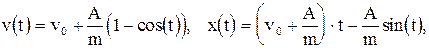
непрерывно зависящее от начальных условий 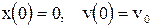 и коэффициентов A, m.
и коэффициентов A, m.
Положим 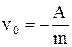 . В этом частном случае решение исходной задачи
. В этом частном случае решение исходной задачи
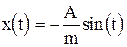
соответствует случаю гармонического колебания точки вблизи ее начального положения. Иными словами, 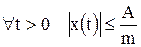 .
.
Очевидно, что при малом отклонении величины v0 от выбранного значения, например за счет погрешности округления данных в ЭВМ, при численном решении задачи получаем (рис. 1)
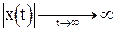 .
.
Таким образом, даже при корректно поставленной задаче ее численное решение может быть связано со значительными трудностями.
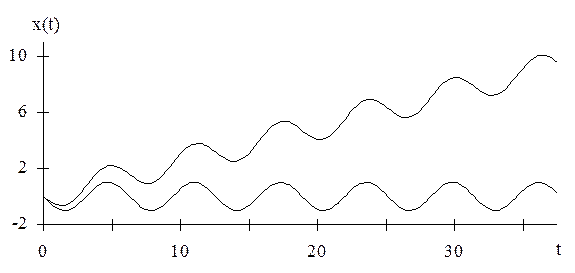
Рис. 1.1. Действительное (нижняя кривая) и возмущенное (верхняя кривая) решения задачи из примера 1.1.
 2015-04-20
2015-04-20 1379
1379







