Пример 7 для трех задач, обсужденных в Примере 7

Проанализируем набор задач с характеристиками, представленными в Таблице 6. Действительно ли результаты такие же, как полученные прямым приложением Теоремы 2?

l Шаг 1. Применяя Шаг 1, мы видим, что единственная рассматриваемая задача - снова Задача 3, таким образом i = 3.

l Шаг 2a. Определите все точки диспетчеризации от 0 до 360 (конец периода задачи самой низкой частоты). Точки диспетчеризации

для Задачи 1: 0, 135, 270

для Задачи 2: 0, 150, 300

для Задачи 3: 0, 360

На оси времени, эти точки диспетчеризации появляются в порядке, представленном на Рисунке 3.

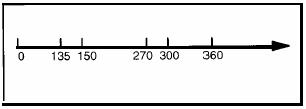
Рисунок 3: Точки диспетчеризации для трех задач, обсужденных в Примере 7.

Шаг 2b. Создайте неравенства для всех точек диспетчеризации. Неравенства:

C₁ + C₂, + C₃ ≤ T ₁

2 C₁ + C₂, + C₃ ≤ T ₂

2 C₁ + 2 C₂, + C₃ ≤2 T ₁

3 C₁ + 2 C₂, + C₃ ≤2 T ₂

3 C₁ + 3 C₂, + C₃ ≤3 T ₃

Шаг 2c. Замените фактическими значениями все переменные, проверьте, выполняется ли хотя бы одно из неравенств. Замены показаны ниже.

45 + 50 + 80 >135

2*45 + 50 + 80 >150

2*45+2*50+80=2*135

3*45+2*50+80>2*150

3*45 + 3*50 + 80 > 360

Заключение. Набор задач из Таблицы 6 - диспетчируем согласно Теореме 2, потому что выполняется одно из неравенств для третьей задачи. Результаты, полученные на Шаге 2c следуют точно за последним столбцом отношений в Решении из Примера 5, который подтверждает применимость эмпирического правила, который мы использовали на сей раз. Есть еще одно ценное замечание, весьма необычное – результат проверки более длинного периода (360, дважды по 150) оказался негативным, а проверка более короткого периода (дважды по 135) – оказалась удачной.

Если понять как работает этот алгоритм может быть весьма забавно искать задачу с наибольшей возможной длительностью периода выполнения и выяснить что система по прежнему диспетчируема.

Это рассматривается в Примере 8[6]