Предел функции
Определение предела функции
Основные понятия и теоремы
Точка a (a 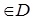 или a
или a 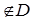 ) называется предельной точкой множества D, если в любой окрестности точки a имеются точки множества D, отличные от a.
) называется предельной точкой множества D, если в любой окрестности точки a имеются точки множества D, отличные от a.
Пример. Рассмотрим множество 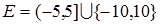 . Предельными точками этого множества являются все точки отрезка
. Предельными точками этого множества являются все точки отрезка 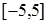 . Точка 10 не является предельной, так как существует окрестность этой точки (например, радиусом 1), в которых нет точек множества
. Точка 10 не является предельной, так как существует окрестность этой точки (например, радиусом 1), в которых нет точек множества 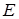 , отличных от самой точки 10. Аналогично, точка –10 не является предельной точкой множества
, отличных от самой точки 10. Аналогично, точка –10 не является предельной точкой множества 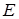 .
.
Пусть функция 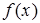 определена на множестве D и a– предельная точка этого множества.
определена на множестве D и a– предельная точка этого множества.
Определение 1 (по Гейне). Число b называется пределом функции 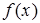 в точке a (или при
в точке a (или при 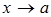 ), если для любой последовательности
), если для любой последовательности 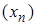 такой, что
такой, что 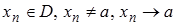 , соответствующая последовательность значений функции
, соответствующая последовательность значений функции 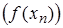 сходится к числу b.
сходится к числу b.
Обозначение: 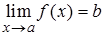 или
или 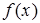
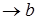 при
при 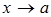 .
.
Пример. Рассмотрим постоянную функцию 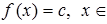 R. Докажем по определению Гейне, что предел этой функции в любой точке
R. Докажем по определению Гейне, что предел этой функции в любой точке 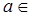 R равен значению функции, т.е. числу с. Выбираем произвольную последовательность
R равен значению функции, т.е. числу с. Выбираем произвольную последовательность 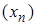 такую, что
такую, что 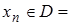 R,
R, 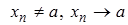 . Строим соответствующую последовательность значений функции
. Строим соответствующую последовательность значений функции 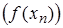 :
: 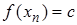 . Получаем, что последовательность
. Получаем, что последовательность 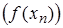 – стационарная, она сходится к числу с. Тогда по определению предела функции по Гейне
– стационарная, она сходится к числу с. Тогда по определению предела функции по Гейне 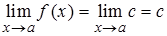
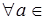 R.
R.
|
|
|
Замечание. Определение предела функции по Гейне справедливо и в том случае, когда элементы 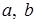 являются
являются 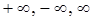 . Например,
. Например,
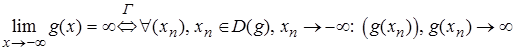 .
.
Определение Гейне основано на понятии предела числовой последовательности, поэтому его часто называют определением “на языке последовательностей”. Существует другое определение предела функции.
Определение 2 (по Коши). Число b называется пределом функции 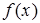 в точке a, если
в точке a, если 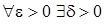 такое, что
такое, что 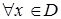 , удовлетворяющего условию
, удовлетворяющего условию 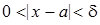 , выполняется неравенство
, выполняется неравенство  .
.
Определение Коши предела функции в точке называют определением ²на языке 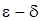 ².
².
Пример. Доказать по определению Коши, что 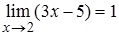 .
.
Выберем произвольное 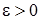 . Задача состоит в том, чтобы для этого
. Задача состоит в том, чтобы для этого 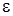 найти такое
найти такое 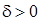 , при котором из неравенства
, при котором из неравенства 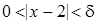 следовало бы неравенство
следовало бы неравенство 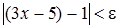 .
.
Преобразуем последнее неравенство: 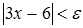 ,
, 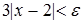 ,
, 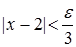 . Получили, что неравенство
. Получили, что неравенство 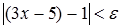 выполняется, если
выполняется, если 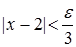 . Отсюда видно, что в качестве
. Отсюда видно, что в качестве 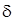 можно взять число
можно взять число 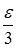 (или любое меньшее). Таким образом,
(или любое меньшее). Таким образом, 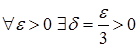 такое, что
такое, что 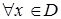 , удовлетворяющего условию
, удовлетворяющего условию 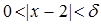 , выполняется неравенство
, выполняется неравенство 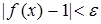 . По определению Коши это означает, что
. По определению Коши это означает, что 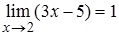 .
.
Теорема 1. Определения предела функции по Коши и по Гейне равносильны.
Используя понятие окрестности, определение предела функции по Коши можно переписать в следующем виде.
Определение 3. Число b называется пределом функции 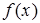 в точке a, если для любой
в точке a, если для любой 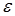 -окрестности точки b существует такая
-окрестности точки b существует такая 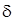 -окрестность точки a, что
-окрестность точки a, что 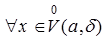
 выполняется
выполняется 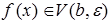 .
.
Cимволическая запись:
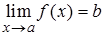
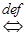
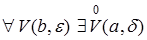
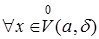 :
: 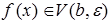 . (1)
. (1)
|
|
|
Определение (3) помогает выяснить геометрический смысл определения предела функции. Рассмотрим график функции 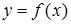 около точки
около точки 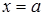 .
.

 Y
Y
| |||||
 | |||||
 |
0 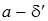
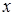
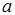
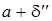 X
X
|
Пределом функции 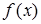 в точке
в точке 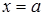 является число b (заметим, что значение функции в точке
является число b (заметим, что значение функции в точке 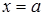 равно
равно 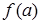 ). Выберем произвольную окрестность точки b радиуса
). Выберем произвольную окрестность точки b радиуса 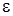 . Согласно определению 3 для этой окрестности
. Согласно определению 3 для этой окрестности 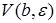 существует окрестность
существует окрестность 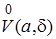 точки
точки 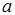 такая, что для любого
такая, что для любого 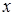 из
из 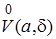 соответствующее значение функции
соответствующее значение функции 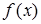 обязательно попадет в окрестность
обязательно попадет в окрестность 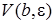 . Докажем существование такой окрестности
. Докажем существование такой окрестности 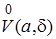 , показав способ ее построения.
, показав способ ее построения.
Через точки  на оси ординат проведем прямые, параллельные оси OX до пересечения с графиком функции. Абсциссы точек пересечения обозначим
на оси ординат проведем прямые, параллельные оси OX до пересечения с графиком функции. Абсциссы точек пересечения обозначим 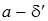 ,
, 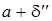 , где
, где 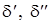 – некоторые положительные числа. Тогда если мы в качестве
– некоторые положительные числа. Тогда если мы в качестве 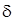 возьмем минимальное из чисел
возьмем минимальное из чисел 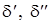 (на рисунке
(на рисунке 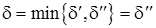 ), то для любого
), то для любого 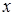 из
из 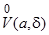 соответствующее значение функции обязательно попадет в выбранную окрестность
соответствующее значение функции обязательно попадет в выбранную окрестность 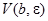 . Если
. Если 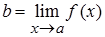 , то такая окрестность
, то такая окрестность 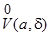 может быть построена указанным способом для любой окрестности
может быть построена указанным способом для любой окрестности 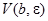 .
.
Так как при фиксированных точках 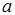 и b окрестности
и b окрестности 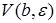 ,
, 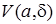 определяются только заданием радиусов
определяются только заданием радиусов 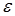 и
и 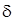 соответственно, то определение 3 в виде (1) можно переписать следующим образом:
соответственно, то определение 3 в виде (1) можно переписать следующим образом:
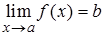
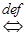
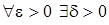
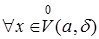 :
: 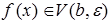 . (2)
. (2)
Определение 3 является общим определением предела функции в том смысле, что в качестве a и b здесь могут быть любые элементы: числа, 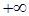 ,
, 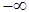 ,
, 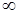 .
.
Пример. Построим определение того, что предел функции 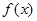 в точке a =–5 равен
в точке a =–5 равен 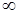 . Согласно определению 3, получаем:
. Согласно определению 3, получаем:
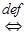
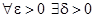
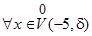 :
: 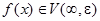 .
.
Используя определение окрестностей 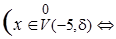
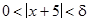 и
и 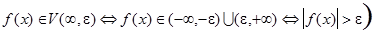 ,
,
получаем: 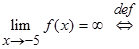
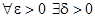 такое, что
такое, что 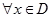 , удовлетворяющего условию
, удовлетворяющего условию 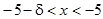 , выполняется неравенство
, выполняется неравенство 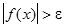 .
.
 2015-05-05
2015-05-05 1205
1205







