Граничные условия Борна-Кармана

Часто удобнее иметь дело с суммами, чем с интегралами. Однако функции, описывающие физические явления в бесконечном кристалле, часто не являются периодическими, т. е. раскладываются в интеграл, а не в ряд Фурье.

Можно считать кристалл конечным (каким он на самом деле и является) и в соответствии с этим ставить для функций естественные граничные условия: например, требовать, чтобы функция обращалась в ноль на границах кристалла. В этом случае функцию можно разложить в ряд на отрезке или в ограниченном объеме (в кубе, например).

Но, во-первых, ограниченность достаточно большого кристалла не сказывается на физических явлениях в объеме, а корректно учесть краевые эффекты и поставить правильные граничные условия обычно непросто.

При этом, кристалл конечного размера уже не обладает трансляционной и точечной симметрией бесконечного кристалла, а использование свойств симметрии часто сильно упрощает решение задачи.

Чтобы рассматривать бесконечный кристалл, но при этом сохранить возможность раскладывать функции в ряды и работать с дискретными величинами, используют искусственный прием: требуют, чтобы функция была периодической по каждой из координат с некоторым большим периодом L. Такие искусственные периодические граничные условия называются условиями Борна-Кармана.

Другими словами, мы делим весь кристалл на большие кубические области с ребром L и требуем, чтобы функция в каждом кубе вела себя одинаково. Такой куб называют нормировочным.

Если L достаточно велико, то такое искусственное ограничение не скажется на физических явлениях, происходящих внутри кристалла, также как не сказывается на них влияние поверхности, если размеры кристалла велики.

Величина L не имеет физического смысла, поэтому окончательное решение задачи не должно зависеть от L при L →∞.

Итак, в соответствии с условиями Борна-Кармана, мы требуем, чтобы функция была периодической по каждой из координат. В трехмерном случае:

Плоская волна удовлетворяет этим условиям только при ''разрешенных'' волновых векторах :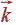

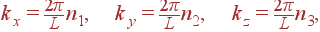
(4)

где n ₁, n ₂, n ₃ — целые числа. В разложении периодической по каждой координате функции будут присутствовать только такие волны.

Разрешенные значения волнового вектора образуют в k -пространстве простую кубическую решетку, двумерный аналог которой изображен на рис. 2.

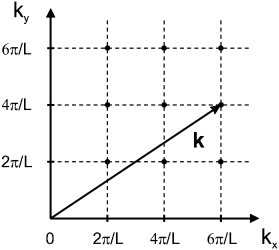Рис. 2.

На каждое разрешенное значение волнового вектора в k -пространстве приходится объем δ ³ k:

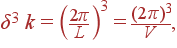
(5)

где V = L ³ — объем нормировочного куба, т. е. куба с ребром L, при V →∞ δ ³ k → 0. Нетрудно посчитать количество разрешенных значений волновых векторов, попадающих в достаточно большой объем k -пространства Δ ³ k:

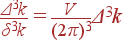
(6)

Пространство волновых векторов называют обратным пространством.

При квантовом описании плоская волна описывает состояние частицы, разные волновые вектора соответствуют разным состояниям Поэтому число разрешенных значений волнового вектора часто называют числом состояний.

Теорема: Если куб достаточно велик, то число состояний, приходящихся на Δ k не зависит от того, какие граничные условия поставлены на границах куба, а определяется лишь его объемом.

Правда, нужно сделать оговорку. Если мы, к примеру, зададим нулевые граничные условия на границах нормировочного куба, то разрешенными состояниями (волнами, по которым раскладывается в ряд функция) будут функции sin k_xx ·sin k_yy ·sin k_zz, с разрешенными компонентами волнового вектора k_x = π n_x / L, k_y = π n_y / L, k_z = π n_z / L. Как видим, интервал между разрешенными значениями k в два раза меньше, чем при периодических граничных условиях, т. е. плотность разрешенных значений волновых векторов в k -пространстве в восемь раз выше. Однако, в этом случае можно считать, что все разрешенные значения компонент k_x, k_y, k_z положительны: волновой вектор (– k_x, k_y, k_z) описывает то же самое состояние, что и (k_x, k_y, k_z). Поэтому здесь мы можем говорить только о количестве разрешенных состояний в объеме Δ k, расположенном в одном из восьми квадрантов k -пространства (с положительными значениями k_x, k_y, k_z). В случае периодических граничных условий, этому объему соответствуют восемь объемов во всех квадрантах k -пространства, таким образом, количество разрешенных состояний будет тем же.

Часто граничные условия, и, как следствие, дискретные разрешенные состояния, возникают непосредственно из условий задачи и имеют явный физический смысл. Например, рассмотренные выше нулевые граничные условия реализуются в кубическом резонаторе, вследствие чего в нем могут существовать волны лишь с разрешенными волновыми числами k_x = π n_x / L, k_y = π n_y / L, k_z = π n_z / L, где L – длина стороны резонатора (между стенками резонатора должно укладываться целое число полуволн).

Те же граничные условия для квантовой частицы в прямоугольной потенциальной яме приводят к тому, что частица может занимать лишь те состояния, для которых между стенками укладывается целое число полуволн Де Бройля, т. е. ее импульс p = ħ k может иметь только разрешенные дискретные значения.

В этих примерах нормировочный объем V уже не является абстрактным объемом, введенным для удобства, а соответствует объему резонатора или потенциальной ямы.

Покажем, как при V →∞ осуществляется переход от суммирования по дискретным состояниям к интегрированию по k -пространству.

Пусть есть сумма по разрешенным значениям k функции 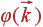. Домножим и разделим эту сумму на δ ³ k = (2 π)³/ V и будем считать, что функция 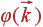почти не меняется на интервале δ k.

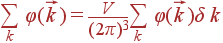
(7)

Предел при δ k → 0 (V →∞) суммы, стоящей в правой части равенства, и есть интеграл:

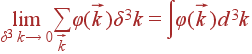
(8)

Отсюда следует правило преобразования суммы в интеграл:

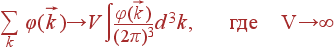
(9)

Итак, на каждое разрешенное состояние в обратном пространстве приходится объем .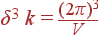

В элементе объема обратного пространства Δ ³ k содержится 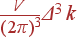разрешенных состояний. Соответственно, 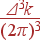— число состояний в элементе Δ ³ k, приходящихся на единицу объема прямого пространства.