По Б.З. Вулих

Основные свойства пространства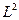

Пространство 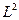- единственное из пространств 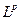, кторое оказывается гильбертовым.

ОПР: пусть 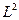означает совокупность всех вещественных измеримых функций 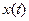, заданных и суммируемых с квадратом на отрезке :

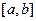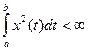
т.е. функция 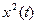должна быть суммируемой. Эквивалентные функции отождествляются. Ясно, что в 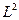входят, в частности, все ограниченные измеримые функции, заданные на 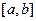, тем более входят все непрерывные функции.

а) Проверим, что множество 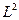- линейная система:

- замкнута относительно опреаций умножения на const и сложения двух элементов из .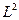

- произведение, будучи всегда суммируемым, может не входить в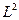

б) Введем норму в 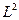по формуле: 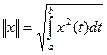- т.о. 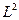- нормированное пр-во

в) Пространство 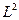также банахово, и притом сепарабельное

г) В 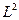можно определить скалярное произведение так, что 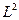оказывается гильбертовым пространством. С этой целью для любых x, y Î 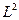положим скалярное произведение (x, y) равным интегралу от произведения этих функций по всему интервалу :

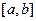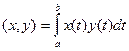
этот интеграл имеет конечное значение для любых x, y Î 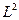. Ясно, что норма и скалярное произведение в 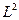связаны соотношением: 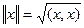. Следовательно, что поскольку пространство 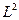полно и сепарабельно, оно является сепарабельным гильбертовым пространством. Кроме того, оно бесконечно-мерно.

Можно рассматривать аналогичное пространство, составленное из функций, суммируемых с квадратом и допускающих комплексные значения. Скалярное произведение вводится:

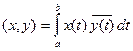
ОПР: метрическое пространство называется полным, если в нем всякая фундаментальная последовательность имеет предел.

ОПР: последовательность точек 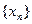метрического прост-ва называется фундаментальной (или сходящейся в себе), есл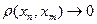и при .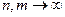

Теорема: если последовательность 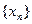сходится к пределу, то она фундаментальна.

Теорема: всякая фундаментальная последовательность 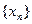ограничена.

Пространства 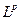при любом 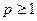полны. В терминах сходимости в среднем это значит, что если последовательность функций 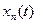из 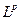сходится в себе в среднем р -того порядка, т.е. есл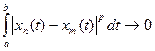и при 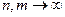, то $ функция из 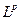, к которой данная послед-ть сходится (тоже в среднем р -того порядка).

ОПР: Мн-во А точек метрического пр-ва Е называется всюду плотным (в Е), если .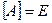

ОПР: Метрическое пр-во называется сепарабельным, если в нем $ счетное или конечное всюду плотное подмножество.

ОПР: Мн-во А точек метрического пр-ва Е называется компактным, если из " бесконечной посл-ти 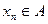можно выделить частичную посл-ть 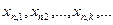(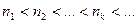), сходящуюся в Е к некоторому пределу.

Теорема: Компактное пространство сепарабельно.

По Колмогоров-Фомин.

Напомним, что скалярным произведением в действительном линейном пр-ве R называется действительная функция 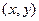, определенная для каждой пары элементов 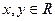и удовлетворяющая следующим условиям:

1)

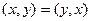
2)

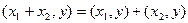
3)

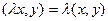
4) 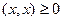причем 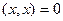только при

ОПР: линейное пространство с фиксированным в нем скалярным произведением называется евклидовым пространством.

В евклидовом пространстве R вводится норма с помощью: .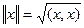

Отметим, что в евклидовом пр-ве сумма, произведение на число и скалярное произведение непрерывны, т.е. если 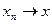, 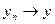(в смысле сходимости по норме), 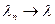(как числовая последовательность), то

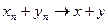
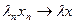
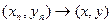
Доказательство этих фактов основано на неравенстве Коши-Буняковского: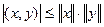

Теорема Фату: Если посл-ть измеримых неотрицательных функций 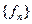сходится почти всюду на А к f и 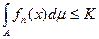, то f интегрируема на А и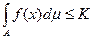

Теорема Фубини: Пусть меры 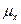и 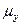определены на s-алгебрах, s-аддитивны и полны; пусть, далее: m = 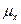Ä 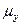и функция 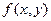интегрируема по мере m на множестве 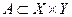Þ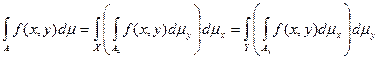

Теорема Радон-Никодим: Пусть m некоторая конечная s-аддитивная мера, определенная на s-алгебре Á подмножеств из Х, а Ф – заряд, определенный на той же s-алгебре и абсолютно непрерывный относительно m. Тогда $ такая суммируемая по m функция f на Х, что

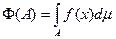
для каждого измеримого А. Эта функция, называемая производной заряда Ф по мере m, определяется однозначно, с точностью до m-эквивалентности (две функции называются m-эквивалентными, если они совпадают почти всюду относительно меры m).

Теорема Лебега (о предельном переходе):

Если посл-ть 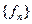на А сходится к f и при всех n 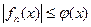, где j интегрируема на А,

то предельная функция f интегрируема на А и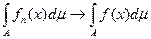

ОПР: Простая (измеримая + не более, чем счетное число значений) функция f называется интегрируемой или суммируемой (по мере m) на мн-ве А, если ряд 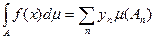, где 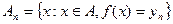абсолютно сходится. Если f интегрируема, то сумма ряда называется интегралом от f по множеству А.