определителей n ГО порядка
1. Метод приведения к треугольному виду.
а) Вычислить определитель: 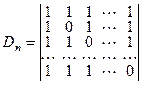 .
.
Вычитая первую строку из всех остальных, получаем определитель, который имеет треугольный вид и, следовательно, равен произведению диагональных элементов:
 . В итоге Dn = (–1) n –1.
. В итоге Dn = (–1) n –1.
б) Вычислить определитель: 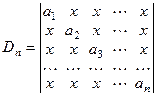 .
.
Вычитаем первую строку из всех остальных, а затем, из столбцов определителя выносим: из первого а 1 – х; из второго а 2 – х; …..; из n го аn – х. Получим:
D = (a 1 – x) (a 2 – x)… (an – x) 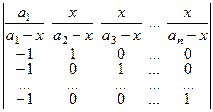 .
.
Запишем первый элемент первого столбца в виде: 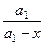 = 1 +
= 1 + 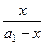 , и все столбцы полученного определителя прибавим к первому столбцу. Получим определитель треугольного вида, который равен произведению диагональных элементов. Следовательно:
, и все столбцы полученного определителя прибавим к первому столбцу. Получим определитель треугольного вида, который равен произведению диагональных элементов. Следовательно:
D = (a 1– x) (a 2 – x)…(an – x) x 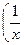 +
+ 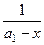 +
+ 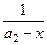 + … +
+ … + 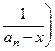 .
.
2. Метод выделения линейных множителей.
а) Вычислить определитель 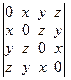 .
.
1. Прибавляя к первому столбцу определителя остальные три, обнаружим, что в первом столбце есть общий множитель, который равен х + у + z. Следовательно, определитель делится на х + у + z.
|
|
|
2. Аналогично, прибавляя к первому столбцу второй и вычитая из него третий и четвертый столбцы, получаем, что определитель делится на х – у – z.
3. Если первый столбец сложить с третьим и вычесть второй и четвертый, то получим, что определитель делится на х – у + z.
4. Если к первому столбцу прибавить четвертый и вычесть второй и третий столбцы, то обнаружим, что определитель имеет множитель х – у + z. Итак:
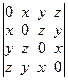 =
=  .
.
Ясно, что определитель является многочленом 4й степени по x, по y и по z. Справа тоже многочлен той же степени. Поэтому V = const. В определитель x 4 входит в слагаемом:
 a 12 a 21 a 34 a 43 = (–1)2× х × х × х × х = х 4.
a 12 a 21 a 34 a 43 = (–1)2× х × х × х × х = х 4.
В правой части старший член по х: Vx 4, т.е. V = 1. Получаем результат:
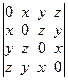 = (x + y + z)(x – y – z)(x – y + z)(x + y – z) = x 4 + y 4 + z 4 – 2 x 2 y 2 – 2 x 2 z 2 – 2 у 2 z 2.
= (x + y + z)(x – y – z)(x – y + z)(x + y – z) = x 4 + y 4 + z 4 – 2 x 2 y 2 – 2 x 2 z 2 – 2 у 2 z 2.
б) Вычислить определитель n -го порядка:  .
.
Этот определитель называется определителем Вандермонда. Рассматривая его как многочлен (n –1)й степени относительно xn увидим, что он обращается в 0 при xn = x 1, xn = x 2, … xn = xn – 1. Тогда Dn = an – 1(xn – x 1)(xn – x 2) … (xn – xn–1), причем an –1 = = Dn –1. Повторяя эту процедуру, получим: Dn = (x 2 – x 1)(x 3 – x 2)(x 3 – x 1)(x 4 – x 3)(x 4 – x 2)(x 4 – – x 1)… = 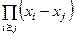 .
.
3. Метод представления определителя в виде суммы определителей.
Вычислить определитель: 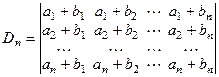 .
.
Заметив, что элементы первого столбца представлены как суммы двух чисел, разложим определитель в сумму двух определителей:
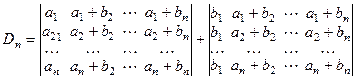 .
.
Теперь каждый из полученных определителей разложим в сумму двух определителей, воспользовавшись тем, что элементы вторых столбцов у них также представлены в виде сумм, и т.д. Проделав это, получим (n > 2), что строки полученных определителей будут такими: ai, ai, …, ai или b 1, b 2, …,bn . Строки 1го типа пропорциональны, 2го типа равны и, следовательно, все слагаемые равны нулю. Следовательно: Dn = 0 (" n > 2).
|
|
|
Для определителей такого же типа, но первого и второго порядков получим:
D 1 = | a 1 + b 1 | = a 1 + b 1; D 2 = 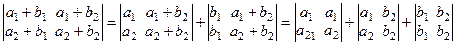 =
=
= a 1 b 2– a 2 b 2 + b 1 a 2 – a 1 b 1 = (a 1 – a 2) b 2 + (a 2 + a 1) b 1 = (a 1 – a 2)(b 2 – b 1).
Метод рекуррентных (возвратных) соотношений.
Вычислить определитель n –го порядка: 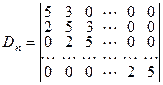 .
.
Разлагая определитель по элементам первой строки, получим рекурентное соотношение: Dn =  .
.
Разложив определитель в правой части соотношения по первому столбцу, запишем новое рекурентное соотношение: Dn = 5 Dn –1 – 6 Dn –2.
Представляя это соотношение в виде: Dn – 2 Dn –1 = 3(Dn –1 – 2 Dn –2) и вводя обозначение:
Тn = Dn – 2 Dn –1 получим: Тn = 3 Тn –1 – 32 Тn –2 = … =3 n-2 T 2=3n.
Аналогично, записав рекурентное соотношение в виде: Dn – 3 Dn –1 = 2(Dn –1 – 3 Dn –2) и обозначая: Vn = Dn – 3 Dn –1 получим Vn = 2 Vn= 1 = 22 Vn –2=…= 2 n.
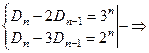 Dn = 3 n + 1 – 2 n + 1.
Dn = 3 n + 1 – 2 n + 1.
В общем случае, для рекуррентных соотношений типа: Dn = pDn – 1 + qDn – 2.можно проделать следующее: пусть a и b корни уравнения x 2 – px – q = 0, т.е. p = a + b,
q = –ab. Тогда Dn = a Dn – 1 + b Dn –1 – ab D n – 2; Dn – a Dn -–1 = b(Dn – 1 – a Dn – 2), т.е. Sn = b Sn – 1 или Dn – b Dn -–1 = a(Dn – 1 – b Dn – 2), т.е. Vn = b Vn – 1.
Аналогично можно поступить и в более сложных рекуррентных соотношениях.
5. Метод изменения элементов определителя.
19°. Если ко всем элементам определителя D добавить одно и то же число x, то определитель увеличится на произведение числа x на сумму алгебраических дополнений всех элементов определителя D.
◀ Пусть D = | aij |; D¢ = | aij + x |. Разложим D¢ в сумму двух определителей относительно первой строки, каждый из них на два относительно второй строки и т.д. Слагаемые, содержащие более одной строки элементов x, равны нулю.
Слагаемые, содержащие одну строку элементов x, разложим по этой строке. Получим D¢ = D + x. ▶
а). 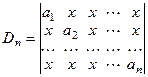 . Вычтем из всех элементов определителя число x
. Вычтем из всех элементов определителя число x
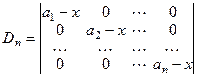 . Тогда Dn = (a 1 – x)(a 2 – x)…(a n – x) + x
. Тогда Dn = (a 1 – x)(a 2 – x)…(a n – x) + x 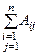 = (a 1 – x)(a 2 – x)...
= (a 1 – x)(a 2 – x)...
…(an – x) + x = (a 1 – x) (a 2 – x) … (an – x) + x 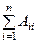 = (a 1 – x)(a 2– x)…(an – x) +
= (a 1 – x)(a 2– x)…(an – x) +
+ x 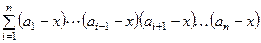 =
=
= x (a 1 – x) (a 2 – x) … (an – x) 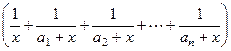 .
.
 2015-05-05
2015-05-05 1357
1357








