Метод гаусса решения системы линейных уравнений. (метод исключения неизвестных)

Решить систему уравнений: .

Записав расширенную матрицу системы, преобразуем ее с помощью преобразований не изменяющих ранг матрицы. Цель: в первом столбце все элементы, кроме одного, должны стать равными нулю. Это равносильно тому, что из 2^го, 3^го и 4^го уравнений будет исключена неизвестная х ₁. Для достижения цели первую строку, умноженную на 2, –3 и –1 прибавим, соответственно, к 2^ой, 3^ей и 4^ой строке. Получим:

~ .

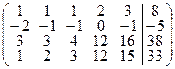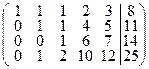Примечание: здесь и в дальнейшем знак ~, стоящий между двумя матрицами означает, что справа и слева от этого знака стоят матрицы одинакового ранга и, следовательно, системы линейных уравнений с такими матрицами имеют одинаковые решения.

Далее вторую строку, умноженную на –1 прибавим к 4^ой строке, тем самым исключив х ₂ из третьего и четвертого уравнений и, наконец исключим х ₃ из 4^го уравнения, прибавив третью строку, умноженную на –1 к четвертой:

~ ~ .

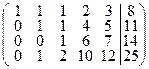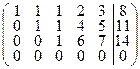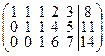Имеем rang A = rang à = 3. Система совместна. n – r =5 –3 = 2, dim L =dim M =2. Так как, размерность пространства решений однородной системы равна 2, то в системе имеется две свободных неизвестных. Выберем в качестве свободных переменных х ₃, х ₄. Отделим в матрице свободные неизвестные вертикальной пунктирной линией: .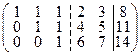

Положив х ₄ = 1, х ₅ = 1, получим х ₁ = х ₂ = х ₃= 1. Т.е. частное решение неоднородной системы (1, 1, 1, 1, 1).

Далее рассмотрим однородную систему уравнений с матрицей 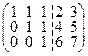. Тогда

.

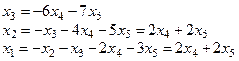Положив х ₄ = 1, х ₅ = 0 Þ е ₁(2, 2, –6, 1, 0). Положив х ₄ = 0, х₅ = 1 Þ е ₂(2, 2, –7, 0, 1), (е ₁, е ₂– ба­зис пространства решений). Отсюда х = (1,1,1,1,1) + a(2,2,–6,1,0) + b(2,2,–7,0,1), где a, b – любые.

Если положить х ₄ = х ₅ = 0, то получим х ₃ = 14, х ₂ = –3, х ₁ = –3, т.е. (–3, –3, 14, 0, 0) еще одно частное решение данной системы. Следовательно, общее решение исходной системы можно записать и в таком виде: х = (–3, –3, 14, 0, 0) + a(2, 2, –6, 1, 0) + b(2, 2, –7, 0, 1), где a, b – любые.

Нужно обратить внимание и на то, что разность двух частных решений неоднородной системы (–3, –3, 14, 0, 0) – (1, 1, 1, 1, 1) есть решение соответствующей однородной системы уравнений.