Неоднородные системы

Рассматривается неоднородная система линейных уравнений Ах = b с n- неизвест-ными.

12°. (Кронекер-Капелли). Система Ах = b совместна тогда, и только тогда, когда ранг главной матрицы системы совпадает с рангом расширенной матрицы rang A =rang à (à = (A|b)).

◀ 1) Пусть система Ах = b – совместна Þ $ с такой, что Ас = b т.е. c ₁S₁ + c ₂S₂ +…+ c_n S _n = b. Таким образом, последний столбец матрицы Ã является линейной комбинацией столбцов матрицы А Þ rang A = rang Ã.

2). Пусть rang A = Ã. Тогда базисные столбцы общие, т.е. являются столбцами матрицы А Þ столбец b является линейной комбинацией столбцов s _1, s _2, …, s_n Þ$ c ₁, c _2, …, c_n такие, что c ₁ S ₁ + c ₂ S ₂ +…+ c_nS_n = b т.е. Аc = b. Система совместна.▶

13°. Если неоднородная система линейных уравнений совместна и rang A = rang à = n,то она имеет единственное решение (по теореме Крамера).

Пусть теперь rang A = rang à = r ≤ n.

14°. Разность двух различных решений неоднородной системы линейных уравнений является решением соответствующей однородной системы, т.е. если c ⁽²⁾ и c ⁽¹⁾ два решения неоднородной системы Ах = b, то c ⁽²⁾ – c ⁽¹⁾ решением однородной системы Ах = 0.

◀ А (c ⁽²⁾ – c ⁽¹⁾) = Аc ⁽²⁾ – Аc ⁽¹⁾ = b – b = 0,т.е. c ⁽²⁾ – c ⁽¹⁾ = c ⁽⁰⁾. Здесь через c ⁽⁰⁾ обозначено некоторое решение однородной системы. ▶

15°. Сумма любого решения однородной системы c ⁽⁰⁾ и некоторого решения неоднородной системы c ⁽¹⁾ есть решение неоднородной системы.

◀ А (c ⁽⁰⁾ – c ⁽¹⁾) = Аc ⁽⁰⁾ + Аc ⁽¹⁾ = 0 + b = b. ▶

Предыдущие два утверждения доказывают теорему об общем виде решения неоднородной системы и линейных уравнений.

16°. Общее решение неоднородной системы уравнений есть сумма общего решения однородной системы и некоторого частного решения неоднородной системы. Эту фразу можно записать с помощью легко запоминающейся аббревиатуры:

О. Р. Н. С. = О. Р. О. С. + Ч. Р. Н. С.

Способ решения неоднородных систем линейных уравнений таков:

1). Если rang A = rang à = n, то решение единственно и может быть найдено по Крамеру;

2). Еслиrang A = rang à = r < n то, записав систему в виде

x ₁ S ₁ + x ₂ S ₂ +…+ x_rS_r = b – x_{r +1} S_{r +1} –…– x_nS_n.

а) положив x_{r +1,} x_{r +2, …,} x_n равными любим фиксированным значениям, получим систему неоднородную (r - уравнений с r -неизвестными) имеющей единственное решение, ибо ее определитель не равен 0. Тем самым будет найдено частное решение неоднородной системы.

b) выбросив вектор b: x ₁ S ₁ + x ₂ S ₂ +…+ x_rS_r = – x_{r +1} S_r+1 –…– x_nS_n и применяя процедуру, описанную в предыдущем параграфе, построим базис в пространстве L решений однородной системы уравнений { e ₁, e₂,..., e_{n – r} }.

с). Тогда x ^{(неодн.)} = x ^{(частн.)} +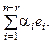

Система векторов { e ₁, e₂,..., e_{n – r} } называется фундаментальной системой решений для системы уравнений Ах = 0.

Если М – множество решений неоднородной системы уравнений, x ^(r)– некоторое частное решение неоднородной системы уравнений, L – пространство решений соответствующей линейной однородной системы, то M = x ^(r)+ L, т.е. М – есть линейное многообразие размерности n – r.