Рассматривается однородная система линейных уравнений с n- неизвестными:
Ах =0 х (х 1, x 2, …, xn).
9°. Если rang A = n, то система имеет только тривиальное решение (х 1 = x 2 = …= xn = 0);
Если rang A < n, то система кроме тривиальных имеет и не тривиальные решения.
◀ Запишем систему Ах = 0 как линейную комбинацию столбцов: x 1 S 1+ x 2 S 2+…+ xnSn =0.
1) rang A = n Þ столбцы S 1, S 2, …, Sn линейно независимы х 1 = x 2 = …= xn = 0 (как коэффициенты тривиальной линейной комбинации линейно независимых векторов).
2) rang A = r < n Þ S 1, S 2, …, Sn – линейно зависимы Þ $ ненулевой набор х 1, x 2,…, xn,такой что x 1 S 1+ x 2 S 2+… + xnSn =0. ▶
10°. Если с (1) и с (2) два различных решения однородной системы Ах = 0, то "a1, a2ÎК a1 с (1)+ a2 с (2)тоже решение той же системы.
◀ Справедливость этого утверждения следует из известного свойства матриц
А (a1 с (1)+ a2 с (2)) = a1 А с (1)+ a2 Ас (2)= 0. ▶
По сути дела теперь можно утверждать, что множество решений однородной системы линейных уравнений образует линейное пространство L.
11°. Размерность пространства L решений линейной однородной системы уравнений Ах = 0 с n -неизвестными удовлетворяет соотношению: dim L = n – rang A.
◀ Пусть rang A = r и S 1, S 2, …, Sr – базисные столбцы матрицы А.
Записав систему Ах = 0в виде x 1 S 1+ x 2 S 2+…+ xrSr = – xr +1 Sr+ 1– xr +2 Sr +2–… – xnSn, отметим, что по набору xr +1, xr +2, …, xn, всегда, и притом однозначно, находятся x 1, x 2, …, xr (по теореме Крамера).
Пусть (c 1, c 2, …, cr, cr +1, …, cn) решение системы Ах = 0.Каждому такому вектору из L поставим в соответствие вектор (cr+1, cr+2,…, cn) из Кn – r .Это соответствие взаимно однозначно в силу сделанного выше замечания. Соблюдается это соответствие и при сложении векторов, и при умножении вектора на скаляр. Таким образом пространства L и Кn – r изоморфны и, следовательно, dim L = dim Кn–r = n – r = n – rang A. ▶
Доказанная только что теорема дает и способ построения базиса в L.
Записав систему Ах = 0в виде x 1 S 1+ x 2 S 2+ … + xrSr = – xr +1 Sr +1– xr +2 Sr +2 –… – xnSn.
1) Положим xr +1 =1, xr +2 = xr +3=… = xn = 0. Найдем 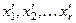 (они существуют и единственны по теореме Крамера). Получим вектор – решение: е 1(
(они существуют и единственны по теореме Крамера). Получим вектор – решение: е 1(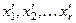 ,1, 0, 0,…, 0).
,1, 0, 0,…, 0).
2) Положим: xr +1 =0, xr +2 =1, xr +3 = … = xn = 0. Найдем 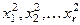 . Получим:
. Получим:
е 2(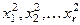 ,0, 1, 0, …, 0).
,0, 1, 0, …, 0).
3) Получим: 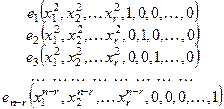 .
.
4) Построенная система векторов линейно независима и образует базис в L.
 2015-05-05
2015-05-05 255
255








