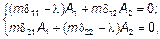
или
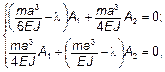
где l – собственные числа.
Упрощаем систему, умножая на 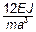 и вводя обозначение
и вводя обозначение 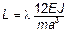 :
:
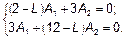 (1)
(1)
Это однородная система линейных алгебраических уравнений относительно амплитуд A 1, A 2. Она имеет ненулевое решение, если ее определитель равен нулю, т. е.
 . (2)
. (2)
Характеристическое уравнение и его решение. Раскрывая определитель (2), получаем характеристическое уравнение
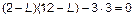 ;
;
или
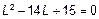 .
.
Дискриминант 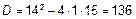 , корни
, корни 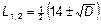 :
:
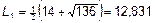 ;
; 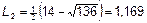 .
.
(Корни нумеруем так, чтобы выполнялось условие L 1 > L 2).
Частоты колебаний. Собственные числа и частоты собственных колебаний связаны соотношением 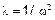 . С учетом обозначения L, введенного в (1), получаем
. С учетом обозначения L, введенного в (1), получаем
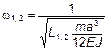 ;
; 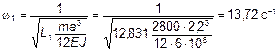 ;
;
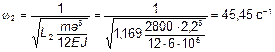 .
.
(Частоты должны быть пронумерованы так, чтобы w1 < w2).
Формы колебаний. Первая форма колебаний соответствует частоте 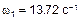 ,
, 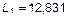 . В системе (1) к L, A 1, A 2 добавляем индекс «1»:
. В системе (1) к L, A 1, A 2 добавляем индекс «1»:
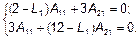 (3)
(3)
Задаемся значением А 11 = 1. Подставляем А 11 и L 1 в (3). Неизвестна всего одна амплитуда А 21, для определения которой можно использовать любое уравнение системы (3), например, первое:
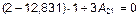 ;
; 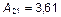 .
.
А 11 – амплитудное значение перемещения y 1 при колебаниях с частотой w1; А 21 – амплитудное значение перемещения y 2 при колебаниях с частотой w1.
|
|
|
Вторая форма колебаний соответствует 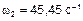 ,
, 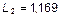 . В системе (1) к L, A 1, A 2 добавляем индекс «2»:
. В системе (1) к L, A 1, A 2 добавляем индекс «2»:
 (4)
(4)
Задаемся значением А 22 = 1. Подставляем А 22 и L 2 в (4). Неизвестна всего одна амплитуда А 12, для определения которой используем второе уравнение системы (4):
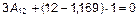 ;
; 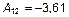 .
.
А 12 – амплитудное значение перемещения y 1 при колебаниях с частотой w2; А 22 – амплитудное значение перемещения y 2 при колебаниях с частотой w2.
Показываем формы колебаний (рисунок 3). Положительные амплитуды откладываем в направлениях, совпадающих с направлениями перемещений y на рисунке 1, отрицательные – противоположно.
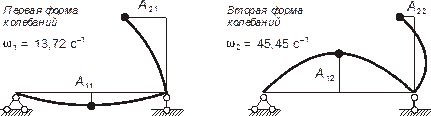
Рисунок 3
Проверка ортогональности форм колебаний. Для рассматриваемой системы с двумя степенями свободы, у которой массы точечных грузов одинаковы, должно выполняться условие
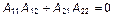 .
.
Подставляя значения амплитуд, получим
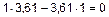 .
.
Проверка выполняется.
þ Пример Расчета системы с тремя степенями свободы
| на свободные колебания Для заданной системы (рисунок 1) требуется: определить частоты и амплитуды собственных колебаний, показать формы колебаний. Исходные данные: масса каждого из точечных грузов m = 2800 кг; длины участков a = 2,2 м, жесткость стержней системы EJ = 6 ∙ 106 Н ∙ м2. | 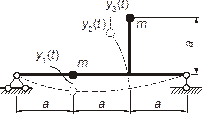 Рисунок 1
Рисунок 1
|
1 Число степеней свободы. Движение из плоскости чертежа считаем невозможным. Вращением грузов пренебрегаем. В соответствии с гипотезой о малости перемещений грузы могут смещаться по перпендикуляру к недеформированной оси рамы. Система обладает тремя степенями свободы, так как перемещения грузов можно полностью описать тремя независимыми величинами y 1(t), y 2(t), y 3(t) (см. рисунок 1).
|
|
|
2 Определение единичных перемещений. В направлении y 1(t) прикладываем единичную силу и строим эпюру 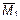 Аналогично строим эпюры
Аналогично строим эпюры 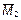 и
и 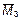 (рисунок 2).
(рисунок 2).
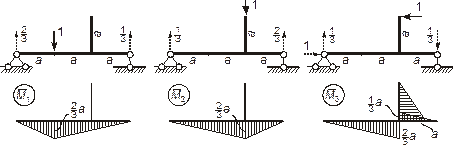
Рисунок 2
Для вычисления перемещений используем формулу Мора:
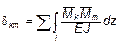 (k, m = 1, 2, 3),
(k, m = 1, 2, 3),
где δ km – перемещение по направлению yk от действия единичного усилия, приложенного по направлению ym; в соответствии с теоремой Максвелла δ mk = δ km.
Перемножив соответствующие единичные эпюры, получим:
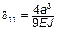 ;
; 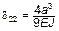 ;
; 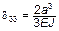 ;
;
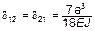 ;
; 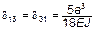 ;
; 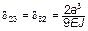 .
.
 2015-05-06
2015-05-06 228
228








