Принцип Лагранжа (Принцип возможных скоростей)

Формулировка ПВС: для равновесия механической системы, на которую наложены стационарные, голономные, идеальные связи необходимо и достаточно, чтобы возможная мощность всех активных сил и моментов активных сил на любом возможном перемещении была равна нулю.

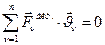( 206)

Доказательство:

1.Необходимость. Докажем ее для ПВП.

Если система находится в равновесии, то

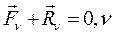=1,2,…,n. (207)

Домножим каждое из этих уравнений на соответствующее возможное перемещение и все уравнения просуммируем:

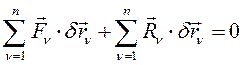. (208)

Поскольку по условию идеальности связей вторая сумма равна нулю, то и первая сумма равна нулю:

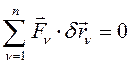
(209)

Необходимость доказана.

2. Достаточность. (Обратная теорема)

Дано: SdA^акт = 0. Доказать, что система находится в равновесии.

Теорема доказывается методом от противного.

Предположим, что SdA^акт = 0, но система не находится в равновесии. Тогда есть сила, нарушающая это равновесие, т.е. .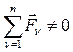

При нулевых начальных условиях перемещение под действием этой силы будет направлено в сторону силы, то есть SdA^акт > 0, что противоречит условию, т.к. нам дано, что SdA^акт = 0. Значит, предположение было неверным, и, система находится в равновесии.

Отметим, что уравнение ПВП часто называют общим уравнением статики, поскольку из него могут быть получены все уравнения статики.

Этот принцип позволяет решать задачи на равновесие методами динамики. Этот принцип был известен со времен Архимеда под названием «золотого правила механики» - выигрыш в силе компенсируется проигрышем в перемещении и наоборот.

8. ПРИНЦИП ДАЛАМБЕРА

Рассматриваемые вопросы:

Принцип Даламбера для материальной точки. Силы инерции. Принцип Даламбера для механической системы. Главный вектор сил инерции. Главный момент сил инерции. Частные случаи приведения сил инерции: при поступательном движении, при вращательном движении вокруг центра масс, при вращении вокруг произвольной оси, при плоском движении, при равномерном вращении однородного стержня. Динамические реакции подшипников при вращении тела около неподвижной оси. Метод кинетостатики. Принцип Даламбера – Лагранжа. Общее уравнение динамики.

8.1 Принцип Даламбера для материальной точки

Рассмотрим движущуюся механическую систему. В составе движущейся системы выделим точечную массу и запишем для нее второй закон Ньютона в виде:

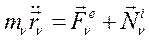(210)

Преобразуем к виду:

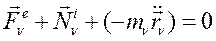(211)

Обозначим:

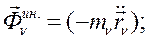(212)

Силой инерции материальной точки называется векторная величина,

равная по модулю произведению массы точки на её ускорение, и направленная противоположно вектору ускорения, .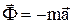

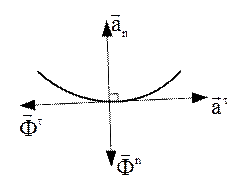
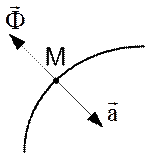
Рис.48

Принцип Даламбера для материальной точки формулируется так: если к фактически действующим на материальную точку активным силам 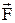и силам реакции связей 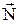добавить фиктивную силу инерции 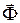, то полученная система сил будет уравновешенной и к ней можно применить уравнения статики:

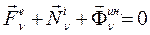. (213)

8.2 Принцип Даламбера для механической системы

По принципу Даламбера для материальной точки:

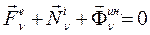
Умножим почленно, векторно это уравнение на 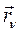, получим векторное произведение:

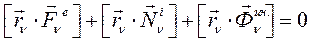(214)

Просуммировав по всем материальным точкам механической системы, уравнения (203) и (204) получим:

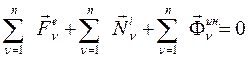(215)

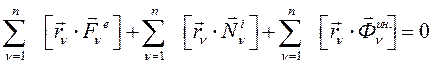(216)

Уравнение (206) представляет собой сумму моментов всех внешних сил, сил реакции (внутренних сил) и моментов сил инерции.

Учитывая, что сумма всех внутренних сил и сумма моментов внутренних сил равна нулю, получим принцип Даламбера для механической системы в виде:

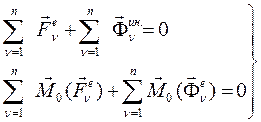(217)

Формулировка: Если в любой момент времени к действующим на механическую систему внешним силам и моментам внешних сил добавить фиктивные силы инерции и моменты сил инерции, получим формально уравновешенную систему сил, для которой можно записать условия и уравнения равновесия.

8.3 Главный вектор сил инерции.

Главный вектор сил инерции – это векторная сумма всех сил инерции, приложенных к телу.

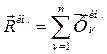(218)

По определению центра масс:

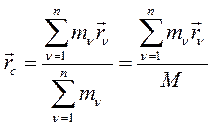(219)

Дважды продифференцируем и преобразовав, получим:

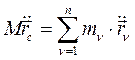(220)

Подставив (220) в (218), получим выражение для главного вектора сил инерции механической системы:

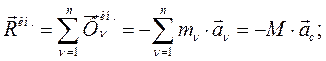(221)

Определение: Главный вектор сил инерции равен произведению массы механической системы на ускорение ее центра масс и направлен в сторону противоположную ускорению центра масс.

8.4. Главный момент сил инерции

Главный момент сил инерции - это векторная сумма моментов всех сил инерции, приложенных к некоторой точке, которую называют центром приведения.

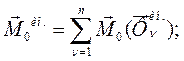(222)

Главный момент сил инерции обычно вычисляют при вращательном движении, поэтому его вычисляют относительно оси вращения.

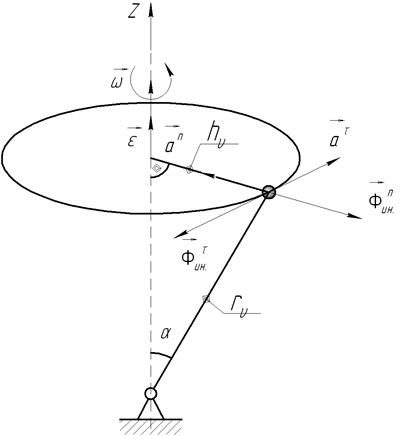
Рис.49

По определению главный момент сил инерции равен:

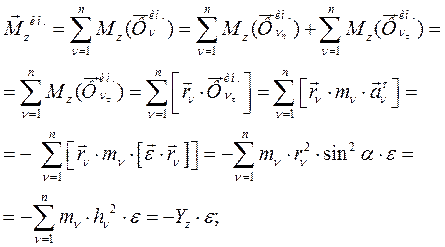(223)

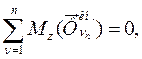так как нормальное ускорение пересекает ось вращения, а это значит, что момент от нормальной силы инерции относительно оси будет равен нулю.

Главный момент сил инерции равен произведению момента инерции тела относительно оси вращения проходящей через центр масс механической системы, на угловое ускорение. Знак минус говорит о том, что главный момент сил инерции направлен противоположно угловому ускорению.

8.5 Силы инерции в частных случаях движения твёрдого тела:

1. Поступательное движение.

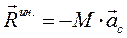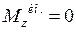, (224)

2. Вращательное движение вокруг оси z, проходящей через центр масс.

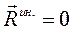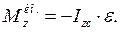, (225)

3. При вращении вокруг произвольной оси.

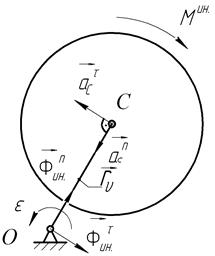
Рис. 50

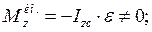(226)

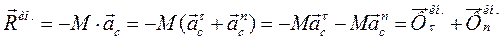(227)

4. Плоскопараллельное движение.

В соответствии с теоремой о разложении плоское движение можно представить как поступательное со скоростью полюса и вращательное вокруг этого полюса. За полюс удобно брать центр масс и прикладывать его в центре масс.

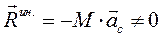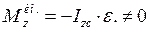, (228)

5. Равномерное вращение однородного стержня вокруг неподвижной оси.

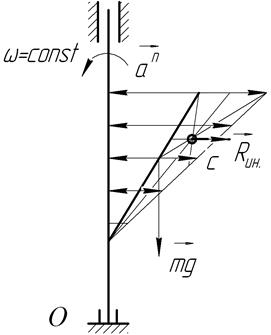
Рис. 51

Сила инерции касательная будет равна нулю, т.к. стержень вращается с постоянной угловой скоростью. Нормальное ускорение тем больше, чем дальше стержень от оси вращения, а поэтому силы инерции нормальные будут также не одинаковыми.

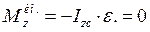(229)

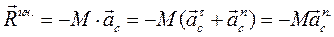(230)

Очевидно, что вектор суммарной силы инерции, оказывающей такое же действие как вся система сил в целом, не будет приложен в центре масс. Суммарный вектор сил инерции будет иметь равнодействующую, которая будет проходить через центр масс эпюры сил инерции, а поэтому 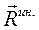отсекает на стержне 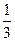длины от удаленного от оси вращения конца стержня.

8.6 Общее уравнение динамики.

Данный принцип является объединением принципов Лагранжа и Даламбера.

Принцип Лагранжа применяется в случае, когда механическая система находится в равновесии, т.е. является необходимым и достаточным условием равновесия

Принцип Даламбера применяется, когда механическая система движется с ускорением, в этом случае добавляя к действующим силам фиктивные силы инерции и их моменты, получают формальное равновесие системы. При равновесии можно использовать не только условия равновесия, но и использовать принцип возможных перемещений. В этом и заключается принцип Лагранжа - Даламбера.

Формулировка: если механическая система, на которую наложены голономные, стационарные, идеальные связи, движется с ускорением, то добавляя к действующим на нее активным силам и их моментам фиктивные силы и моменты сил инерции, получим формально уравновешенную систему сил, для которой можно применить принцип возможных перемещений.

Применяя к механической системе одновременно принцип Даламбера и принцип возможных перемещений, придём к зависимости: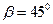

SdA_ν^а +SdA_ν^Ф +SdA_ν^r = 0 (231)

Но так как для идеальных связей сумма виртуальных работ всех сил реакции равна нулю (SdA_ν^r = 0) то получим общее уравнение динамики в виде:

SdA_ν^а +SdA_ν^Ф =0. (232)

При движении системы, подчинённой удерживающим идеальным связям, сумма элементарных работ всех приложенных активных сил и всех сил инерции на любом возможном перемещении системы будет равна нулю.

В аналитической форме общее уравнение динамики имеет вид:

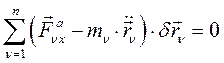(233)

9 УРАВНЕНИЯ ЛАГРАНЖА ВТОРОГО РОДА

Рассматриваемые вопросы:

Обобщенные координаты скорости, ускорения и возможные перемещения. Представление кинетической и потенциальной энергии в квадратичной форме. Обобщенные силы и методы их вычисления. Вывод уравнений Лагранжа второго рода из общего уравнения динамики. Физический смысл уравнений Лагранжа второго рода. Функция Лагранжа. Принцип возможных перемещений в обобщенных координатах. Уравнения Лагранжа второго рода для консервативных механических систем.

9.1 Обобщенные координаты, скорости, ускорения, возможные перемещения.

а) Определение: Обобщенными координатами называются любые независимые параметры, однозначно определяющие положение механической системы в пространстве:

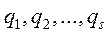- их число «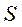» равно числу степеней свободы (ЧСС).

Обобщенными скоростями называются первые производные по времени от обобщенных координат:

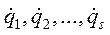(их число равно ЧСС).

Обобщенными ускорениями называются вторые производные по времени от обобщенных координат или первые производные по времени от обобщенной скорости:

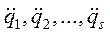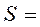( ЧСС)

Обобщенными возможными перемещениями называются первые вариации от обобщенных координат:

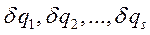(S = ЧСС)

Обобщенные координаты, скорости, ускорения и возможные перемещения связаны с обобщенными координатами, скоростями, возможными перемещениями через радиус вектор:

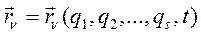(234)

Дифференцируя по времени, получим:

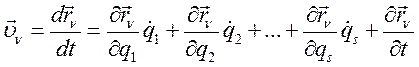(235)

Или:

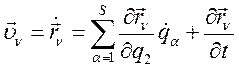(236)

Для обобщённых возможных перемещений, варьируя по времени, получим:

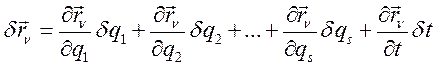(237)

Так как время фиксировано, то 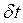=0

Таким образом, формула взаимосвязи имеет вид:

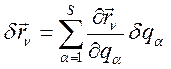(238)

Пример:

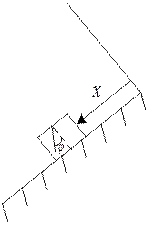
Рис. 52

Число степеней свободы этой механической системы равно двум. Введем обобщенные координаты:

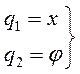
9.2 Обобщенные силы.

а) Определение: обобщенными силами называются коэффициенты при обобщенных возможных перемещениях в формуле виртуальной работы, т.е. по аналогии с обычными силами:

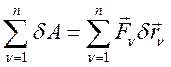(239)

Получим:

(240)

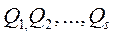- обобщенные силы.

Число обобщенных сил равно 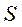. Обобщённые силы векторами не являются, это проекции сил, проекции моментов сил и другие силовые характеристики.

б) Общая формула для вычисления обобщенных сил:

По определению виртуальных работ:

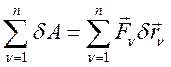(241)

Подставим в эту формулу, формулу взаимосвязи (228) и меняем порядок суммирования:

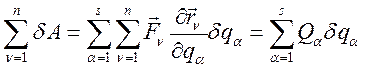(242)

Т.е. 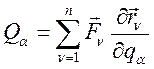- обобщенные силы 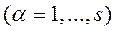(243)

Эта формула позволяет вычислять обобщенные силы во всех случаях, но она неудобна для использования.

в) Практическая формула для определения обобщенных сил.

По определению:

(244)

Пусть необходимо определить 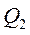, для этого дают соответствующей обобщенной координате 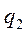положительное приращение, т.е. дают возможное перемещение 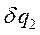>0 (т.е. направленное в сторону увеличения 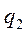), считая все остальные обобщенные координаты в данный момент времени фиксированными, неизменными: т.е. 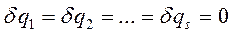, тогда:

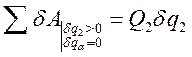- практическая формула для вычисления .

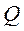Пример:

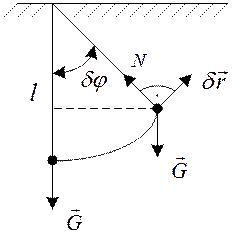
Рис. 53

Даём координате 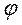приращение 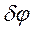>0.

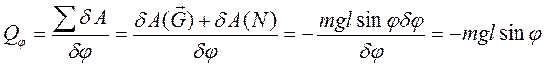
-это момент относительно точки подвеса.

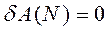(, т.к. )

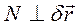г) Обобщенные силы в потенциальном поле.

По определению потенциального поля:

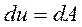
По определению потенциальной энергии 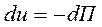, отсюда:

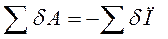, но потенциальная энергия это функция от координат, т.е. 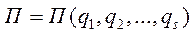и тогда:

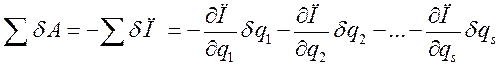(245)

Отсюда: 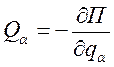- обобщенные силы в потенциальном поле.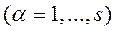

9.3 Принцип обобщенных возможных перемещений.

По определению принципа:

«Для равновесия механической системы с наложенными идеальными, голономными, стационарными связями необходимо и достаточно, чтобы:

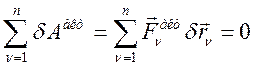, но:

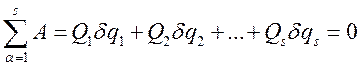(246)

Это равенство нулю возможно при любых «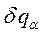» только в этом случае, если одновременно все коэффициенты при 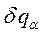равны нулю.

Т.е. 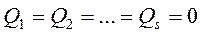- принцип обобщенных возможных перемещений.

Формулировка: Для равновесия механической системы с наложенными на неё идеальными, голономными, стационарными связями необходимо и достаточно, чтобы одновременно все обобщенные силы были равны нулю.

9.4 Уравнение Лагранжа второго рода.

Выведем из общего уравнения динамики:

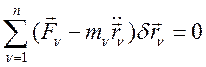(247)

Подставим в эту формулу, формулу взаимосвязи:

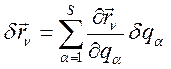(248)

Меняя порядок суммирования, получим:

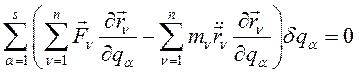(249)

Обозначим:

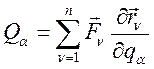, (250)

Учитывая, что

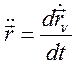(251)

и подставив в формулу (250) и (251) в (249) получим:

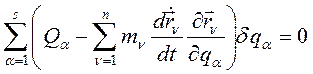(252)

Преобразуем: 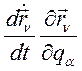Вынесем 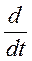, получим:

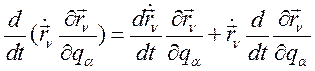(253)

или:

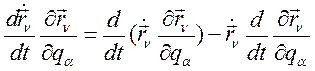. (254)

Подставим (254) в (252):

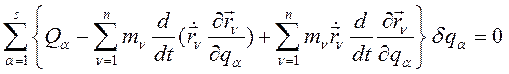(255)

Используем формулы, известные из курса математического анализа:

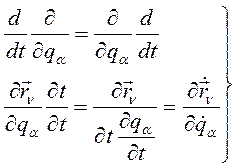(256)

Подставим (256) в (255):

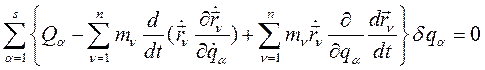(257)

Преобразуем, внесем 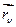под знак частной производной:

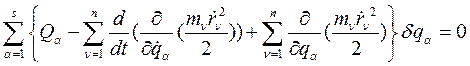(258)

Заменим 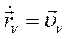, получим:

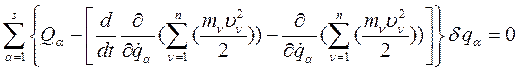(259)

Заменим:

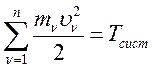(260)

Получим:

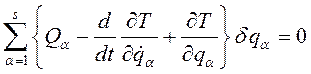(261)

При произвольных бесконечно малых 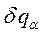это равенство нулю возможно только в этом случае, когда все коэффициенты при бесконечно малом возможном перемещении 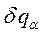одновременно будут равны нулю. Отсюда:

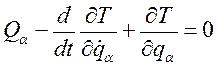(262)

Уравнение Лагранжа второго рода имеет вид:

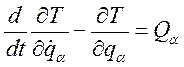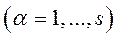- (263)

Разность полной производной по времени от частной производной от кинетической энергии механической системы по обобщенной скорости и частной производной от кинетической энергии механической системы по обобщенной координате равна обобщенной силе.

Выводы:

1. Уравнение Лагранжа второго рода это дифференциальные уравнения второго порядка в обобщенных координатах.

2. Число уравнений Лагранжа второго рода равно числу степеней свободы.

3. Уравнения Лагранжа второго рода носят интегральный характер, т.к. эти уравнения содержат только характеристики всей системы и не содержат характеристик отдельных материальных точек.

4. В эти уравнения не входят силы реакции, которые всегда неизвестны, их можно не обозначать на чертеже.

5. Физический смысл уравнений Лагранжа второго рода.

Пример:

Точка движется по горизонтальной плоскости по закону x=x(t):

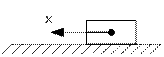
Рис. 54

Число степеней свободы механической системы равно единице. Введем обобщенную координату q=x. Тогда: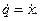

Кинетическая энергия механической системы: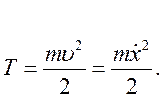

Уравнение Лагранжа второго рода имеет вид:

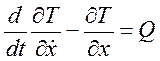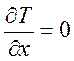, , так как кинетическая энергия является функцией скорости, то получим:

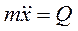- это второй закон Ньютона. Таким образом, уравнения Лагранжа второго рода это обобщенный вид второго закона Ньютона.

9.5 Уравнения Лагранжа второго рода в потенциальном поле.

Общая формула уравнений:

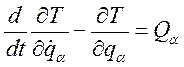(264)

Обобщенная сила в потенциальном поле:

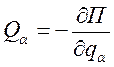(265)

Подставим:

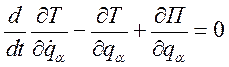(266)

Вынесем 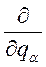, получим:

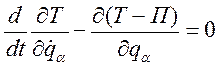(267)

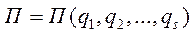, так как потенциальная энергия является функцией координат и 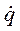в потенциальную энергию не входит, тогда можно записать:

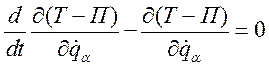(268)

Введем обозначения:

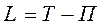(269)

Уравнение Лагранжа второго рода в потенциальном поле имеет вид:

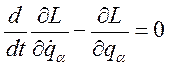(270)

9.6 Функция Лагранжа.

Функции Лагранжа называется разность между кинетической и потенциальной энергией:

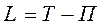
Физический смысл функции Лагранжа в том, что она выражает физическое состояние механической системы в данный момент времени и поэтому её называют функцией состояния механической системы или кинетическим потенциалом.

Математический смысл: Функция Лагранжа это функция от обобщенных координат, обобщенных скоростей и времени.

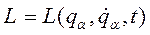, т.е. в общем случае это функция 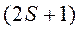переменных.