Двухфазная система с отказами

Пусть заявки, образующие простейший поток с интенсивностью λ, обслуживаются двухфазной системой обслуживания (например, двумя приборами, бригадами, системами и т.п.). Распределение времени обслуживание на обоих фазах полагаем экспоненциальными с параметрами m₁ и m₂, соответственно: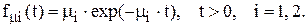

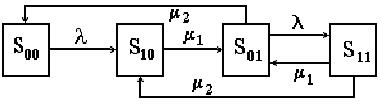
Рис. 13.1

Множество возможных состояний системы: S₀₀ - система свободна; S₁₀ - первый прибор занят, второй свободен; S_0A - второй прибор занят, первый свободен; S₁₁ - оба прибора заняты. Размеченный граф состояний системы представлен на рис. 14.1.

Обозначим заявку, появившуюся первой заявкой A, а заявку, появившуюся второй - заявкой B.

Правила функционирования системы:

- Если обслуживание заявки A на первой и второй фазе оканчивается до прихода следующей заявки (заявки B), то состояние системы меняются в последовательности S₀₀→ S₁₀→ S_0A→ S₀₀.

- Если в момент, когда первый прибор был занят обслуживанием заявки A (состояние S₁₀), пришла следующая заявка (заявки B), то заявка B получает отказ и покидает систему.

- Если заявки B поступает в момент, когда заявки A перешла во вторую фазу обслуживания (S_0A), то система переходит в состояние S₁₁ с интенсивностью λ (переход S_0A→S₁₁): заявка A находится на второй фазе обслуживания, заявки B находится на первой фазе обслуживания).

Из состояния S₁₁ процесс обслуживания быть продолжен по двум вариантам.

- Если обслуживание заявки B на первой фазе окончится раньше, чем освободится второй прибор, то она получает отказ в обслуживании на второй фазе и покидает систему с интенсивностью μ₁ (переход S₁₁→S_0A). Прерванное обслуживание считается эквивалентным отказу в обслуживании. Таким образом, вероятность обслуживания заявки оказывается меньше вероятности приема к обслуживанию.

- Если обслуживание второй фазы первой заявки окончится раньше, то заявки A покидает систему обслуженной, а в системе остается только вторая заявка на первой фазе обслуживания (переход S₁₁→S₁₀ с интенсивностью μ₁).

Система однородных линейных уравнений для предельных вероятностей составляется по размеченному графу состояний па известным правилам:

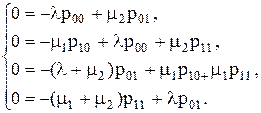
Заменив одно из уравнений однородной системы (скажем, третье уравнение), уравнением нормировки (p₀₀+ p_0A+ p₁₀₊ p₁₁=1), получим систему линейных уравнений, которая в матричной форме имеет вид:

.

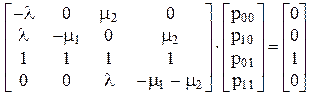Из этой системы можно найти выражения для вероятностей всех состояний и необходимые критерии эффективности системы.