1. Периодическая последовательность прямоугольных импульсов (рис.2.14).
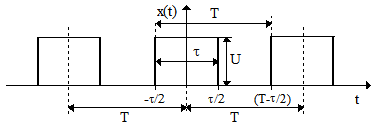
Рис.2.14
Основные параметры последовательности импульсов: U - амплитуда; t - длительность; T - период. Дополнительные параметры:
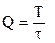 - скважность,
- скважность, 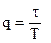 - коэффициент заполнения.
- коэффициент заполнения.
Математическая запись в форме аналитической функции:
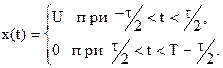
На основании формулы (2.4.3) для прямого преобразования Фурье найдем комплексный спектр
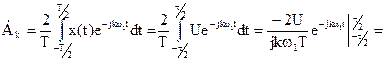
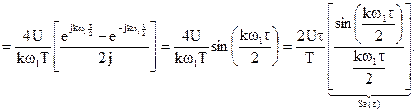
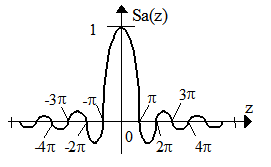
Рис.2.15
Выражение в квадратных скобках обозначим как 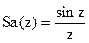 - функция отсчетов (рис.2.15), принимающая нулевые значения в точках
- функция отсчетов (рис.2.15), принимающая нулевые значения в точках 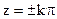 при k=1,2,...
при k=1,2,...
Итак, 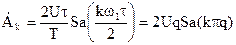 , так как
, так как  .
.
Из формулы видно, что 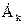 - действительная величина
- действительная величина 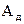 . Такую величину можно представить в виде одного графика (рис.2.16).
. Такую величину можно представить в виде одного графика (рис.2.16).
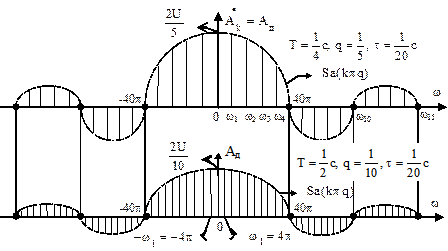
Рис.2.16
Пусть параметры сигнала T=1/4c, t=1/20c и q=1/5. Тогда для первого графика на рис.2.16 имеем: wk=kw1=2kp/T=8kp; w1=8p, w2=16p, w3=24p, w4=32p, w5=40p; Sa(kpq)=Sa(kp/5)=0 при k=5, 10, 15,... Первый нуль функции отсчетов будет в точке 40p на частоте w5=40p.
Изменим параметры сигнала: T=1/2c, t=1/20c и q=1/10. Тогда для второго графика на рис.2.16 получим wk=4kp и Sa(kpq)=Sa(kp/10)=0 при k=10, 20, 30,... Здесь первый нуль функции отсчетов будет также в точке 40p, но на частоте w10=40p. В результате на интервале 40p в отличие от первого графика размещаются 10 спектральных линий, включая нулевую в точке 40p.
|
|
|
Пример показывает, что с увеличением периода T частота основной гармоники 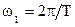 уменьшается. В результате растет число гармоник на фиксированном интервале частот, например [0,40p]. Другими словами, с увеличением T спектр становится плотнее. При этом амплитуды гармоник уменьшаются. Форма огибающей спектра не изменяется. Она зависит только от формы импульса.
уменьшается. В результате растет число гармоник на фиксированном интервале частот, например [0,40p]. Другими словами, с увеличением T спектр становится плотнее. При этом амплитуды гармоник уменьшаются. Форма огибающей спектра не изменяется. Она зависит только от формы импульса.
В пределе при T ® ¥ имеем одиночный импульс, т.е. непериодический сигнал. Спектр при T ® ¥ становится сплошным и имеет вид огибающей спектра периодической последовательности импульсов.
Пример также показывает, что спектр четной функции x(t) - действительная функция, для описания которой достаточен один график.
Спектр нечетной функции x(t) - комплексная функция. Для описания этого спектра нужны два графика - спектр амплитуд и спектр фаз.
2. Одиночный прямоугольный импульс (рис.2.17).
Это непериодический сигнал. Аналитическая форма его записи:
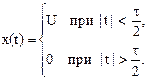
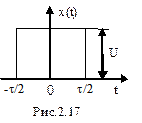
Интегральное преобразование Фурье функции x(t) имеет вид
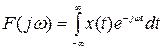 ;
;
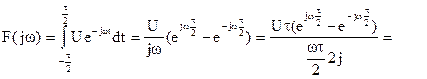
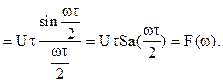
Спектральная функция является действительной функцией, т.е. F(jw)=F(w). Значит, спектр может быть представлен одним графиком (рис.2.18).
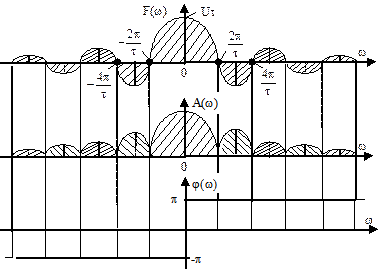
Рис.2.18
Так как F(w) - знакопеременная функция, то переход к амплитудному спектру (рис.2.18)
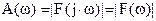
требует введения фазового спектра, несмотря на то, что функция
j(w) = 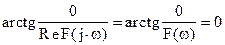 ,
,
иначе потом исходный сигнал x(t) не восстановить.
3. Функция отсчетов (рис.2.19).
 x(t)= Sa(wct)
x(t)= Sa(wct) 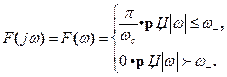
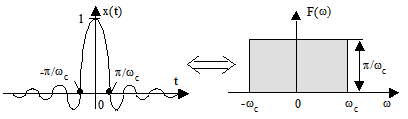
Рис.2.19
Сравнение преобразования Sa(wct)ÛF(jw) с п.2.6.2 показывает еще одно свойство преобразования Фурье - свойство взаимности. Переменные t и w взаимно заменимы.
|
|
|
4. Односторонний экспоненциальный импульс.

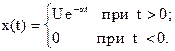
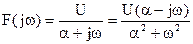 .
.
Спектральная функция комплексна, так как x(t) - нечетная функция. Для ее представления нужны два графика - амплитудный и фазовый спектры (рис.2.20).

Рис.2.20
5. Единичный импульс (или дельта-функция).
Введем понятие дельта-функции. Рассмотрим прямоугольный импульс D(t) (рис.2.21).
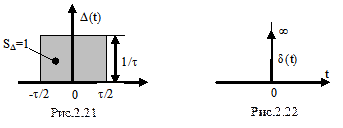
Для него условие нормировки имеет вид
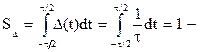 единичная площадь.
единичная площадь.
Устремим t® 0. Функция 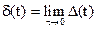 называется дельта-функцией или единичным импульсом (рис.2.22). Согласно определению,
называется дельта-функцией или единичным импульсом (рис.2.22). Согласно определению,
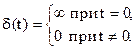
Площадь d-импульса 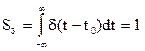 (условие нормировки).
(условие нормировки).
Эта функция является абстрактным понятием, а именно математической идеализацией.
Дельта-функцию можно сдвигать по оси времени (рис.2.23). В общем случае
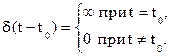
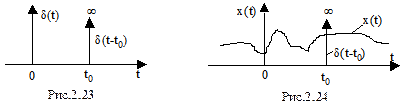
Дельта-функция (рис.2.24) обладает фильтрующими свойствами, т.е.
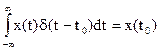 .
.
Очевидно, при t0=0 имеем
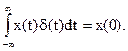
Рассмотрим спектральное представление d-функции (рис.2.25):

Рис.2.25
Дельта-функция имеет равномерный спектр. Она содержит все частоты с одинаковой плотностью амплитуд.
Единичный импульс, т.е. d-импульс, широко используется как испытательный сигнал. Согласно обратному преобразованию Фурье его можно записать и в такой форме:
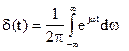 .
.
6. Постоянная функция (рис.2.26).
Эта функция абсолютно неинтегрируемая, но в пределе имеет преобразование Фурье:
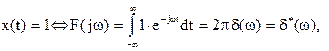
где 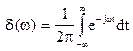 - дельта-функция в частотной области.
- дельта-функция в частотной области.

Рис.2.26
7. Сигнум-функция (рис.2.27).
Это абсолютно неинтегрируемая функция, но в пределе имеет преобразование Фурье:
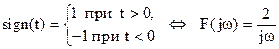 .
.

Рис.2.27
8. Единичная функция (рис.2.28).
Эта функция абсолютно неинтегрируемая, но имеет преобразование Фурье. Часто используется как испытательный сигнал:
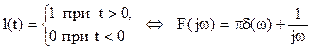 .
.
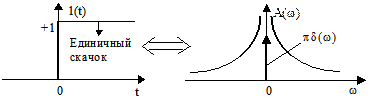
Рис.2.28
Связь между дельта-импульсом и единичной функцией:
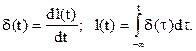
9. Гармонический бесконечный сигнал Acosw0t, tÎ[-¥,¥].
Представление этого сигнала в форме рядов Фурье (рис.2.29):
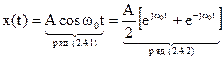 .
.
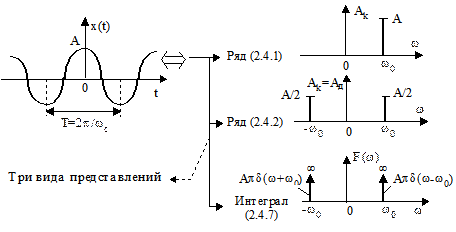 Рис.2.29
Рис.2.29
Эта функция абсолютно неинтегрируемая, но в пределе имеет интегральное преобразование Фурье (рис.2.29):
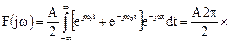
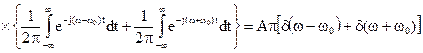 .
.
10. Косинусоидальный импульс (рис.2.30).
Аналитически он представляется как D(t)cosw0t, где D(t) - видеоимпульс прямоугольной формы.
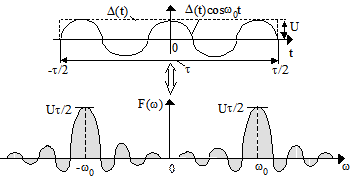
Рис.2.30
 2015-05-06
2015-05-06 2816
2816








