Понятие измерения

В зависимости от предметной области, условий проведения экспертизы и конкретной ситуации эксперты непосредственно или опосредованно выражают свое мнение о значимости тех или иных характеристик объектов рассмотрения, распределяют варианты по определенным группам, сравнивают объекты по обозначенным характеристикам. Сложность такого рода деятельности обусловлена тем, что относительно оцениваемых характеристик, которые могут иметь самую различную, в первую очередь качественную природу, часто испытывается существенный дефицит сведений. Добывание этих недостающих сведений и преследуется экспертами.

Каждый из экспертов выражает свое личное, вообще говоря, субъективное мнение, которое часто отличается от мнения других участников экспертизы высказанных при ответе на один и тот же вопрос в одинаковых ситуациях (в общем случае «сколько экспертов, столько и оценок»). Чтобы эффективно работать со спектром мнений, результаты опроса экспертов целесообразно выражать в как можно более удобной форме. Например, при оценивании результатов фигурного катания на льду, руководствуясь определенными правилами и собственным впечатлением, каждый эксперт (судья) может вполне подробно и аргументировано обосновать свое мнение. На соревнованиях же выступает несколько фигуристов, и сравнивать многословные характеристики всех фигуристов крайне проблематично. Поэтому поступают следующим образом: каждый судья должен высказать свое мнение в концентрированном виде – в установлении определенного количества баллов. Тот из фигуристов, кто получит наибольшее количество баллов, тот и победитель (упорядочив полученные баллы, автоматически получают распределение мест для всех участников).

Для целевого изменения формы исходных результатов оценивания характеристик применяются соответствующие операции, получившие название измерение. По своей сущности измерение есть совокупность операций, направленная на установление соответствия между значением измеряемой характеристики и некоторым «эталонным» множеством (чисел, цифр, имен и других групп символов, имеющих в данном случае определенный смысл). Тем самым может быть установлена значимость (мощность, вес) рассматриваемой характеристики, выраженной с помощью этих эталонов.

Установление такого рода соответствия далеко не тривиальная процедура. Она выполняется по вполне определенным правилам и существенно зависит от природы измеряемой характеристики и применяемых технологий.

Все мы привыкли под измерением понимать результаты сравнения данной характеристики с некоторой единицей. Допустим, что оценивается площадь садового участка. Тогда в процессе измерения пытаются установить, сколько стандартных единиц площади (обычно квадратных метров) соответствует площади этого участка. Так если участок имеет площадь 826 квадратных метров, это означает, что она в восемьсот двадцать шесть раз больше, чем площадь квадрата со стороной один метр, называемой «один квадратный метр». Такого рода измерения в основном применяются для оценивания геометрических и физических характеристик (длины, объема, веса, мощности, скорости, …).

На практике часто приходится сталкиваться и с принципиально другими ситуациями. Допустим, градусник на внешней стороне окна показывает пять градусов по Цельсию (5⁰ С), а подобный градусник внутри комнаты показывает 20⁰ С. В этой ситуации не говорят, что в комнате в четыре раза теплее, чем на улице (это высказывание лишено смысла). Однако сказать, что на улице на пятнадцать градусов – вполне допустимо. Другой пример. Два студента сдавали экзамен. Один получил оценку отлично, а второй – удовлетворительно. Очевидно, что первый показал знания существенно лучшие, чем второй, однако вопрос: на сколько лучше? – не корректен. Еще один пример: оценивается цвет волос. Если спрашивают, у кого из двух индивидуумов более светлые волосы, то возможны ответы: у первого, у второго или одинаковы. Если же спрашивают, является ли данный человек брюнетом, то возможно услышать ответ или «да» или «нет». В том случае, когда такой вопрос будет задан относительно всех студентов данной учебной группы, то подобная деятельность экспертов позволит отделить брюнетов от всех остальных. Даже эти простейшие примеры свидетельствуют о том, что в каждом конкретном случае к задачам измерения следует подходить внимательно и в зависимости от ситуации действовать соответствующим способом. Каким? На этот вопрос призвана отвечать теория измерения, изложенная во многих работах (см. например, работы [99][100]. В данном изложении мы будем опираться на работу[101].

Как и в целом ряде других случаев, в теории измерений разрабатываются некоторые модели, которые могут использоваться при выполнении вполне определенных условиях. Задача пользователя состоит в том, чтобы выбрать и использовать одну из них, предварительно обосновав достаточную степень ее адекватности решаемой задаче. Роль моделей в теории измерений играют шкалы.

В самом общем случае шкалой измерения называется множество 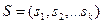объектов произвольной природы, называемых пунктами шкалы, с заданной на этом множестве совокупностью отношений 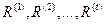, составляющих структуру данной шкалы. Следовательно, шкала – это следующий картеж .

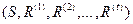Содержательно измерение в данной шкале можно представить как процедуру подбора для данной оценки характеристики определенного пункта выбранной шкалы, т.е. элемента 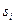из 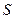(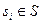). При этом принципиально важным является то обстоятельство, что рассматриваемые в данной экспертизе характеристики удовлетворяют всей совокупности отношений 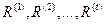. Лишь только в таком случае все полученные от экспертов оценки некоторой характеристики могут быть измерены в данной шкале. Это означает, что в последующем вместо этих оценок можно оперировать соответствующими пунктами шкалы. Какими могут быть эти операции? Только те, при которых сохраняется условия выполнимости отношений шкалы измерений .

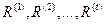Примечание. В качестве пунктов шкалы удобнее использовать числовые обозначения. Всегда ли эти обозначения можно рассматривать, как математические объекты под названием числа? Нет, далеко не всегда. Только в тех случаях, когда измеряются количественные характеристики. Если измеряют качественные характеристики, им можно сопоставлять лишь числовые имена, но проводить с ними те же операции, что и с числами (как математическими объектами) нельзя.

С наиболее общей точки зрения для любой шкалы можно проследить общие основы ее математического описания. Вне зависимости от типа шкалы объекту a из некоторого множества однотипных объектов сопоставляется степень проявления Q _a - его рассматриваемой характеристики: a → Q _a. Подчеркнем, что именно Q _a является результатом деятельности экспертов.

Совокупность возможных степеней проявления (уровней) {Q _a } образует множество эмпирических данных. С этими данными производятся процедуры измерения (оценки, идентификации), т.е. выявляется множество значений {q(a)}, называемых результатом измерения. В случае числовых показателей q(a) есть число, которое определяется в соответствии с используемой единицей измерения [Q]. Что же касается показателей, измеряемых в нечисловых шкалах, то для них результаты процедуры измерения являются элементами некоторого (нечислового) множества заданных эталонных степеней проявления данного показателя (пунктов используемой шкалы). В таком качестве могут выступать и числовые метки, используемые для кодировки и обозначающие соответствующую степень проявления качества или имя класса (для номинального показателя).

Измерение (в широком смысле) есть процедура, сопоставляющая каждому элементу некоего эмпирического множества A определенный элемент некоего абстрактного структурированного множества S. Для нечисловых шкал в качестве множества S выступает множество имен классов или заданных уровней качества, а для числовых шкал – числовое множество возможных результатов измерения данной величины. Процедуру измерения условно можно изобразить в следующем виде

а: Q _a → q(a) → φ(q(a)).

Как уже отмечалось, множество 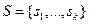пунктов шкалы могут составлять объекты как числовой, так и нечисловой природы. Если пунктам шкалы сопоставлены не числа, то каждое из них может быть закодировано числовым именем. Например, при обработке анкет для показателя «пол» используются имена «мужской» и «женский». Ясно, что эти именам можно сопоставить любые два числа, например, 0 и 1 соответственно. Обозначив такого рода сопоставления через 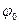, можем записать

.

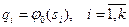При этом принципиально важным является требование сохранения свойств исходной шкалы, носителями которых выступает ее структура. Для выполнения этого требования отношениям 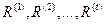должны отвечать вполне определенные заданные на 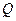такие, заданные на множестве 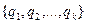, отношения 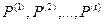, что отображение 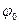должно удовлетворять условию

.

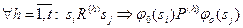Для данной шкалы отображение 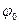не единственно. Возможно любые отображения 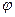, которые сохраняют отношения 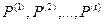. Этот факт можно записать в следующей форме

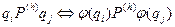
Допустимыми преобразованиями над числовыми метками 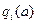будут являться такие взаимооднозначные функции 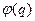, что

.

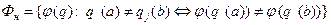Можно показать, что для каждой конкретной шкалы может быть сформировано соответствующее множество 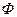всех взаимно-однозначных функций допустимых в рамках данной шкалы преобразований, т.е. тех, которые не меняют соотношений между объектами измерений, а именно

.

Рассмотрим некоторые аспекты классификация измерительных шкал.

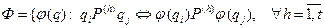1. В зависимости от мощности множества 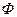шкалы классифицируют по мощности. Более мощные шкалы обладают всеми возможностями шкал менее мощных, что связывает все шкалы в единую систему измерений

2. Шкалы разделяют на два основных класса: метрические (в которых может быть установлена числовая единица измерения, например, килограмм, градус, рубль) и неметрические(если единицы измерения не могут быть установлены).

Метрические шкалы являются более мощными, поскольку отражают больше информации о различии измеряемых объектов. К неметрическим шкалам относят номинативные (шкалы наименований) и порядковые шкалы.

3. Для классификации шкал устанавливают наличие (или отсутствие) следующих главных атрибутов:

· Упорядоченность. Если одна позиция шкалы, определяемая числом и соответствующая выраженности измеряемого свойства, больше, меньше или равна другой позиции, то говорят, что эта шкала упорядочена;· Интервальность. Если шкала обладает интервальностью, то это означает, что интервалы между позициями шкалы равны между собой;· Наличие или отсутствие нулевой точки (или точки отсчета). Если шкала имеет нулевую точку отсчета, обозначаемую за 0, то ей соответствует объект, у которого измеряемое свойство полностью отсутствует.

Отметим, что только в номинативной шкале отсутствуют все главные атрибуты измерительных шкал, а именно упорядоченность, интервальность и нулевая точка.

Далее рассмотрим наиболее распространенные шкалы измерений в порядке возрастания множество их возможных преобразований.

4.2.2. Шкалы измерений числовых показателей.

Рассмотрение типов шкал начнем с так называемой а бсолютной шкалы, (шкалы натуральных чисел). Эту шкалу образует множество действительных чисел и отношение тождества. Все остальные преобразования запрещены. В этой связи для абсолютной шкалы имеем

Ф _а = { φ(q) = q }.

Данные, полученные с помощью абсолютной шкалы, не преобразуются (каждое число тождественно только самому себе), т.е. шкала тождественна сама себе, поэтому она и получила такое название. Строго говоря, только для абсолютной шкалы результаты измерений могут выражаться натуральными числами. Поэтому абсолютные шкалы применяются для измерения количества объектов, когда нет никакого сомнения в наличии неясностей относительно измеряемой оценки. Наиболее характерным примером применения абсолютной шкалы может явиться оценка количества людей в данном помещении (их количество всегда сожжет быть выражено натуральным числом). В этой шкале может быть измерено и число решенных в ходе выполнения контрольной работы задач, количество вагонов в составе поезда или деталей при сборке компьютера и т.п.

Если оценка характеристики измерена в абсолютной шкале, то это свидетельствует о том, что относительно этой операции эксперт обладает исчерпывающей информацией. В этой связи абсолютная шкала является наиболее сильной шкалой. Из дальнейшего изложения станет понятным, что абсолютная шкала – это частный случай шкалы интервалов.

Перейдем к рассмотрению шкалы, которая чаще всего используется для измерения физических характеристик. При традиционном понимании термина «измерение» предполагается, что физическая величина Q может в различной степени проявляться и быть зафиксированной для различных объектов, которые этой величиной характеризуются. Предполагается также, что выделено некоторое фиксированное значение [Q] степени проявления данной величины, которое называют «единица меры» величины Q. Тогда задача измерения величины Q при помощи единицы меры [Q] заключается в нахождении числового множителя q в равенстве Q = q [Q], при этом Q и [Q] считаются положительными скалярными величинами одного и того же рода, а множитель q - положительное действительное число.

Пусть a – объект, обладающий некоей степенью проявления физической величины Q. Эту степень будем обозначать Q _a. Например, пусть a – данный металлический стержень, тогда Q _a – длина этого стержня. Измерить длину стержня a с помощью единицы измерения [Q] – значит определить такое значение q (a) множителя q, что

Q _a = q (a) [Q]. (1)

В общем виде традиционное измерение можно рассматривать как процедуру, которая степени проявления Q _a величины Q у объекта a сопоставляет числовое значение (действительное число) q (a):

Q _a → q (a). (2)

Иначе говоря, число q (a) показывает, сколько единиц Q содержит в себе Q _a.

Множество всевозможных значений таких чисел q (a) составляет шкалуизмерения физической величины Q с заданной единицей измерения [Q]. Заметим, что Q _a – физическая величина (длина данного стержня), то есть именованное число, обладающее той же размерностью, что и сама величина Q (стрежень), в то время как q (a) – безразмерное числовое значение.

Результаты измерения физической величины должны удовлетворять следующему достаточно очевидному требованию: а именно, реально существующим соотношениям между различными степенями проявления величины Q должны отвечать соответствующие отношения между результатами измерения. Так, если стержень a имеет длину, бóльшую чем длина стержня b, то и между результатами измерения этих длин должно выполняться аналогичное отношение:

Q _a 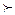Q _b => q (a)> q (b). (3)

Примечание. Важно различать используемые в соотношении (3) знаки: знак 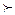обозначает большую степень проявления реальной характеристики (в данном случае длины), тогда как знак > выражает обычное числовое неравенство в значении «больше».

Аналогичным образом при суммировании длин стержней a и b (в реальности это может быть достигнуто, если, например, один стержень приставить к другому) общая длина при измерении должна дать результат, равный сумме результатов измерения длин q (a) и q (b):

Q _a Å Q _b → q (a)+ q (b). (4)

В (4) знак Å - операция над физическими объектами, тогда как знак + означает обычное суммирование действительных чисел.

Покажем, что какова бы ни была выбрана единица измерения [Q] показателя «длина» отношение результатов измерения длин двух стержней остается неизменным. В самом деле, пусть длины стержней a и b были измерены вначале с использованием единицы измерения [Q⁽¹⁾]:

Q _a = q ₁(a) [Q⁽¹⁾], Q _b = q ₁(b) [Q⁽¹⁾],

а затем с использованием единицы измерения [Q⁽²⁾]:

Q _a = q ₂(a) [Q⁽²⁾], Q _b = q ₂(b) [Q⁽²⁾].

Пусть измерение единичной (для первой шкалы) длины [Q⁽¹⁾] по шкале с единицей измерения [Q⁽²⁾] дает результат

[Q⁽¹⁾] = q ₀ [Q⁽²⁾]. (5)

Тогда, как легко видеть, в силу (2.5) q ₂(a) = q ₀ q ₁(a); q ₂(b) = q ₀ q ₁(b), и таким образом

q ₁(a) / q ₁(b) = q ₂(a) / q ₂(b), (6)

что и требовалось доказать.

Последнее соотношение выражает тот факт, что свойство стержня a «быть во столько-то раз длиннее» стержня b не зависит от той конкретной шкалы, по которой измерялись их длины.

Итак, какова бы ни была шкала измерения характеристики «длина», отношение результатов измерения двух данных объектов (в смысле числовой дроби) остается постоянным. Этим объясняется то, что шкалы, обладающие этим свойством, называют шкалами отношений. Примеры измерений в этой шкале: деньги, меры длины, объема, веса и т.п.

Мы установили, что для этих шкал преобразование результатов измерения q (a) с помощью функций вида

φ(q) = k q, (7)

где k – произвольно выбранное положительное число, сохраняет свойство (6). Так же как показатель «длина», в шкалах отношений измеряются такие показатели, как «масса» (в граммах, килограммах, тоннах и т. д.), «длительность промежутка времени» (в секундах, часах, годах и т. д.), «стоимость» (в рублях, копейках, долларах и т. д.). Для различных степеней проявления этих величин также несложно определить операцию суммирования Å, которая будет связана с результатом измерения q (a) соотношением (4).

Общим характерным свойством для показателей, измеряемых в шкалах отношений, является то, что они обладают естественной «нулевой» степенью проявления, когда результат измерения q(a) равен нулю. В относительной шкале (ratio scale) присутствуют все атрибуты измерительных шкал: упорядоченность, интервальность, нулевая точка.

Из (6) и (7) видно, что для этих показателей имеет смысл утверждение о том, что степень проявления величины Q у одного объекта во сколько-то разбольше, чем у другого. Как будет показано далее, для шкал других типов такого рода утверждения не являются осмысленными, поскольку их истинность или ложность может зависеть от выбранного конкретного преобразования результатов измерения.

Для показателей, измеряемых в шкалах отношений, любые другие преобразования результатов измерения, отличные от (7), приводят к нарушению свойства (6). Например, пусть преобразование результатов измерения q (a) производится с помощью функций вида

φ(q) = k q + l, (8)

где k и l – любые действительные числа. Чтобы выполнялось условие (6), должно быть

φ(q (a)) / φ (q (b)) = q (a) / q (b).

Однако равенство

k q (a) + l / k q (b) + l = q (a) / q (b)

будет справедливо для любых q (a) и q (b) только в случае, если l = 0, то есть для преобразований вида (7).

Для величин, измеряемых по шкале отношений преобразования вида φ(q) = k q, играют особую роль: только они сохраняют важное характерное отношение между различными степенями проявления данной величины, а именно «быть во столько-то раз больше».

По сложившейся терминологии говорят, что преобразования вида (7) образуют множество допустимых преобразований для шкалы отношений.

Таким образом, для шкалы отношений имеем

Ф _о = { φ(q) = k q; " k > 0 }. (9)

В некотором роде эквивалентной шкале отношений является ш кала разностей. В отличие от шкалы отношений, она не имеет естественного нуля, но имеет естественную масштабную единицу измерения. Классическим примером этой шкалы является историческая хронология. Некоторые исследователи, например, полагают, что Иисус Христос родился за четыре года до общепринятого начала нашего христианского летосчисления (… от рождества Христова). Сдвиг на четыре года назад ничего не изменит в хронологии. Можно использовать мусульманское летосчисление или же считать годы от сотворения мира. Кому как нравится. В этом она сходна со шкалой интервалов. Разница лишь в том, что значения этой шкалы нельзя умножать (делить) на константу. Поэтому считается, что шкала разностей — единственная с точностью до сдвига.

Следовательно, для шкалы разностей имеем

Ф _р = { φ(q) = q+l; " l 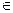R }.

Поскольку в повседневной деятельности мы чаще всего встречаемся с характеристиками, измеренными в шкале отношений, то может сложиться впечатление, что характеристические свойства, выраженные условиями (6) и (7), присущи всем величинам, непосредственно измеряемым в числовой форме. Однако это далеко не так.

Рассмотрим, например, показатель Q - «температура», измеряемая в градусах Цельсия. Казалось бы, свойства шкалы измерения этого показателя те же, что и для рассмотренного ранее показателя «длина»: имеется единица измерения ([Q] = 1^о); кроме того, с помощью измерения можно получить ответ на вопрос о том, на сколько единиц температуры одно тело теплее, чем другое (так же, как и для длины: на сколько единиц длины один объект длиннее, чем другой).

Пусть согласно определению (2) q ^(С)(a), q ^(С)(b), q ^(С)(c), q ^(С)(d) – результаты измерения температуры объектов a, b, c, d в градусах Цельсия. Покажем, что утверждение «различие между температурой объектов a и b в k раз больше, чем различие между температурой объектов c и d»

q ^(С)(a) - q ^(С)(b) = k (q ^(С)(c) - q ^(С)(d)) (10)

является осмысленным, то есть сохраняет свою истинность и при переходе к другой шкале измерения температуры. Например, как известно, результаты измерений в шкалах Цельсия q ^(С) и Фаренгейта q ^(F) связаны между собой следующим соотношением:

q ^(F) = 9/5 q ^(С) + 32. (11)

Следовательно,

q ^(F)(a) - q ^(F)(b) = (9/5 q ^(С) (a)+ 32) - (9/5 q ^(С) (b)+ 32) = 9/5 (q ^(С)(a) - q ^(С)(b)) =

= 9/5 k (q ^(С)(c) - q ^(С)(d)) = k (9/5 q ^(С)(c) – 9/5 q ^(С)(d)) =

= k {(9/5 q ^(С)(c) +32) – (9/5 q ^(С)(d) +32) }

и таким образом

q ^(F)(a) - q ^(F)(b) = k (q ^(F)(c) - q ^(F)(d)),

что и требовалось показать. Более того, легко видеть, что истинность данного утверждения сохраняется при любом линейном преобразовании шкалы измерения температуры вида (8), частным случаем которого является соотношение (11).

Таким образом, для показателя «температура» соотношения между степенями его проявления вида

Q _a - Q _b = k (Q _c - Q _d) (12)

сохраняют свою истинность, в какой бы температурной (конкретной) шкале этот показатель ни измерялся.

Что же касается самих результатов измерения, то для них вопрос о том, во сколько раз теплее (холоднее)один объект по сравнению с другим, оказывается бессмысленным, что сразу же говорит о том, что свойства шкалы измерения данного показателя отличаются от свойств шкал отношений.

Итак, для таких показателей, как температура, результаты измерения обладают характеристическим свойством, которое может быть представлено соотношением вида (10), не меняющим свою истинность при любых преобразованиях вида (8). Оно было названо интервальным преобразованием, т.к. сохраняет отношение подобия для интервалов показателей (см. 12.) В этой связи шкалы измерения таких показателей носят название шкалы интервалов. Их отличительной особенностью является то, что они (как и шкала отношений) имеют единицу измерения но, в отличие от последней, не имеют фиксированного начала отсчета.

Отсутствие фиксированного начала отсчета может быть объяснено тем обстоятельством, что величины данного типа не обладают естественно выраженной «нулевой» степенью своего проявления.

Множество допустимых преобразований Ф_и для шкал интервалов имеет вид

Ф_и = { φ(q) = k q + l; " k, l (k > 0) }. (13)

Помимо температуры (измеряемой по Цельсию, или по Фаренгейту, или по Реомюру[102]) примером показателя, измеряемого по шкале интервалов, может служить «историческая дата» (дата выпуска единицы продукции, дата исторического события, дата рождения человека и т. п.). В самом деле, свойство (10) для исторических дат не изменится, будем ли мы измерять даты в годах от рождества Христова или в веках от сотворения мира, или в неделях от Французской революции. Примерами шкал измерения исторических дат служат юлианский, грегорианский и мусульманский календари.

Сравнивая шкалу отношений и шкалу интервалов, мы находим, что класс допустимых операций для второй из них более узкий (разности результатов измерения можно делить друг на друга, а сами результаты измерений – нет). В то же время (точнее говоря, за счет этого), множество допустимых преобразований у шкалы интервалов (13) шире, чем у шкалы отношений (9).

Абсолютная шкала, шкала отношений, шкала разности и шкала интервалов позволяют представить результаты измерения количественных показателей.

Отметим также, что в отличие от шкалы отношений шкала интервалов допускает отрицательные значения результатов измерения (в силу того, что параметр l в (13) может быть как положительным, так и отрицательным числом). Примерами могут, очевидно, служить отрицательные температуры, а также даты исторических событий «до рождества Христова (до нашей эры)».

За счет дальнейшего расширения множества допустимых преобразований Ф мы получаем возможность представления результатов измерения нечисловых (качественных) показателей.