Если f (x) непрерывна на [ a, b ] и f (а) f (b) < 0, то $ c Î [ a, b ]: f (c) = 0.
Доказательство:
Пусть для определённости f (а) < 0, f (b) > 0. Тогда, в силу устойчивости знака непрерывной функции, найдётся правая полуокрестность точки а, в которой f (x) < 0.
(рисунок)
Рассмотрим множество Х таких точек 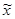 Î[ a, b ], что f (x) < 0 на [ a,
Î[ a, b ], что f (x) < 0 на [ a, 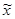 ).
).
X ={ 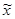 :
: 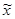 Î[ a, b ], f (x) < 0 на [ a,
Î[ a, b ], f (x) < 0 на [ a, 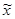 )}.
)}.
Это множество непустое, ограниченное сверху и, следовательно, имеет точную верхнюю грань:
с º sup X. Отметим, что " x < c: f (x) < 0. (1)
Докажем, что f (с) = 0.
Допустим, что это не так.
Предположим, что f (с) > 0. Тогда Þ f (x) > 0 в некоторой окрестности точки c, и, следовательно, (рисунок)
$ x < c: f (x) > 0, что противоречит (1).
Предположим, что f (с) < 0. Тогда f (x) < 0 в некоторой окрестности точки с.
(рисунок)
Следовательно, $ 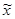 > c: f (x) < 0 на [ a,
> c: f (x) < 0 на [ a, 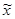 ), а это противоречит тому, что c = sup X.
), а это противоречит тому, что c = sup X.
Значит, наше предположение неверно, и f (c) = 0.
 2015-04-20
2015-04-20 885
885








