Интегральный признак сходимости ряда с положительными членами

Теорема 13.7. (теорема Коши-Макларена). Пусть функция f (x) неотрицательна и не возрастает всюду на полупрямой x ³ m, где m – любой фиксированный номер. Тогда числовой ряд

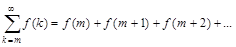(1)

сходится тогда и только тогда, когда существует предел при 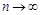последовательности

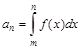(2)

Доказательство. Пусть k – любой номер, удовлетворяющий условию k ³ m + 1, а x – любое значение аргумента из сегмента 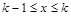. Т.к. по условию f (x) не возрастает на указанном сегменте, то для всех x из указанного сегмента справедливы неравенства

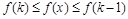(3)

Функция f (x) ограниченна и монотонна, следовательно интегрируется на сегменте 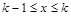. Более того, из (3) вытекает, что

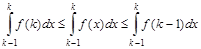или

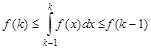(4)

Неравенства (4) установлены для любого номера k ³ m + 1. Запишем эти неравенства для значений 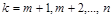, где n – любой номер, превосходящий m.

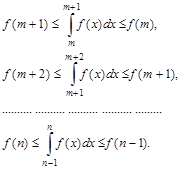
Складывая почленно записанные неравенства, получим

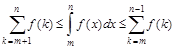(5)

Договоримся обозначать символом S_n n -ю сумму ряда (1), равную

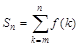(6)

Учитывая (2) и (6), неравенства (5) можно переписать следующим образом

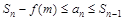(7)

Неравенства (7) позволяют доказать теорему. Из формулы (2) очевидно, что последовательность 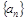является неубывающей. Следовательно, для сходимости этой последовательности необходима и достаточна ее ограниченность. Для сходимости ряда (1) необходима и достаточна ограниченность последовательности 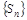. Из неравенства (7) следует, что последовательность 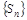ограничена тогда и только тогда, когда ограничена последовательность 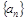, т.е. когда последовательность 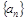сходится.