Признак Лейбница сходимости числового ряда

Признак Лейбница относится к так называемому знакочередующемуся ряду. Ряд называется знакочередующимся, если члены этого ряда поочередно имеют то положительный, то отрицательный знаки

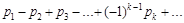(1)

где все p_k ³ 0.

Теорема 13.14 (признак Лейбница). Если члены знакочередующегося ряда, взятые по модулю, образуют невозрастающую бесконечно малую последовательность, то этот ряд сходится.

Доказательство. Пусть дан ряд (1) и известно, что последовательность 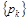является невозрастающей и бесконечно малой. Частичную сумму этого ряда четного порядка 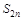можно записать в виде

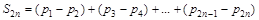(2)

Т.к. каждая скобка в (2) неотрицательна, то при возрастании n последовательность 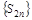не убывает. С другой стороны, 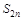можно переписать в виде

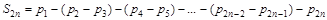, (3)

откуда очевидно, что для любого номера n будет 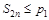. Таким образом, последовательность частичных сумм не убывает и ограничена сверху. В силу Теоремы 3.15 ( Теорема 3.15. Если неубывающая (невозрастающая) последовательность ограничена сверху (снизу), то она сходится.) эта последовательность сходится к некоторому числу S, т.е. 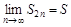. Из очевидного равенства 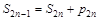и из того, что 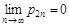, вытекает, что и последовательность нечетных частичных сумм 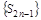сходится к S, т.е. 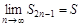. Таким образом, вся последовательность 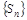сходится к S.