Обратное интерполирование

Одним из важных аспектов применения интерполяционной формулы Лагранжа является решение так называемой задачи обратного интерполирования — нахождения приближенного значения 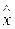по известному значению 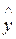. Речь здесь пойдет, в первую очередь, о таблично заданных функциях, для которых 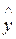не совпадает ни с одним узлом. Формально можно поступить следующим образом: построить обратную функцию 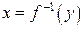и по заданному 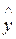найти 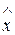по формуле

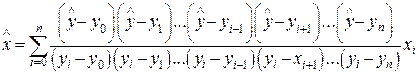(39)

т.е. поменяв в формуле (9) значения функции и аргумента. Это нетрудно проделать для многочленов небольших степеней, однако процесс заметно усложняется при увеличении степени. Если же степень многочлена заранее неизвестна, то наиболее приемлемы интерполяционные формулы Ньютона, Бесселя и Стирлинга.

Поступаем следующим образом. Выбираем базовый узел 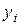, наиболее близкий к заданному значению 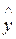. Предполагая, что функция 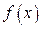монотонна, а 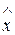находим допуская его близость к 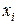, т.е. его находят из соответствующих интерполяционных формул путем последовательных приближений (итераций) длины интервала 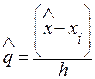, из которого следует .

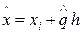Пусть, например, 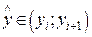, т.е. находится в середине диагональной таблицы разностей, и, следовательно, применима любая из центральных интерполяционных формул. Из формулы

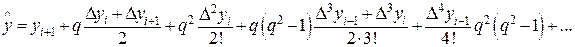
выражаем

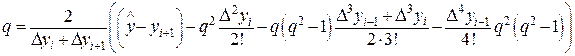
и строим итерационный процесс

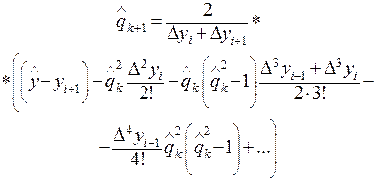(40)

при k= 0, 1, 2…, начиная с 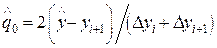. Количество членов в формуле (37) можно зафиксировать в соответствии с поведением конечных разностей, а сам итерационный процесс продолжаем до выполнения условия 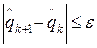, где e - наперед заданная погрешность вычисления.

Аналогичные формулы можно получить исходя, из других интерполяционных выражений. Например, если 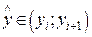и находится в начале диагональной таблицы разностей, то подходящей для обратного интерполирования итерация будет

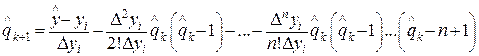(41)

Пример 5. Пусть функция y=y (x) задана в виде таблицы (см. пример 4 из предыдущего параграфа). Требуется найти приближенно корень уравнения y= 0 с точностью e =0,01.