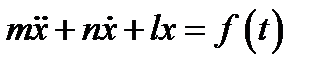 (4.1)
(4.1)
Рассмотрим горизонтально расположенную пружину с закреплённым левым концом. На правом конце пружины приклеплен груз массой m.
Обозначим точку отсчета 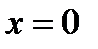
(в этом положении пружина не растянута). Обозначим
через 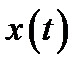 положение груза в момент времени
положение груза в момент времени 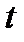 , как обычно через
, как обычно через 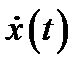 обозначим скорость,
обозначим скорость,
через 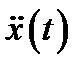 ускорение груза. Обязательно указываем физический закон, которому удовлетворяет
ускорение груза. Обязательно указываем физический закон, которому удовлетворяет
пружина. Это закон Гука. Считаем, что в момент времени 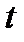 на массу m действует сила упругости пружины равная (
на массу m действует сила упругости пружины равная (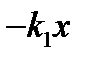 ), сила сопротивления среды (например пружина находится в жидкой среде)(
), сила сопротивления среды (например пружина находится в жидкой среде)(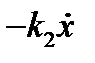 )и некая внешняя сила растягивающая пружину
)и некая внешняя сила растягивающая пружину 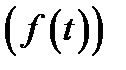 . По второму закону Ньютона
. По второму закону Ньютона
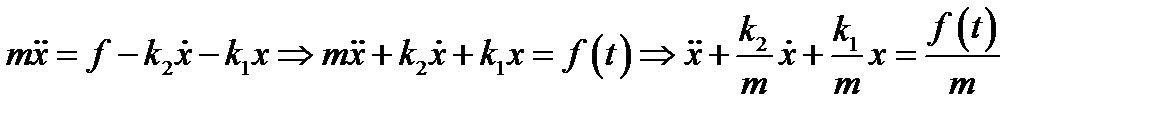
Пусть верхний конец пружины приклеплён к потолку, а к нижнему концу прикреплён груз массой m. Посмотрим, как будет выглядеть уравнение движения груза в этом случае. Пусть ось координат ОУ направлена вертикально вниз и 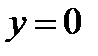 положение грузика в нерастянутом состоянии. Под действием силы тяжести пружина растянется и упругая сила пружины уравновесит вес груза:
положение грузика в нерастянутом состоянии. Под действием силы тяжести пружина растянется и упругая сила пружины уравновесит вес груза: 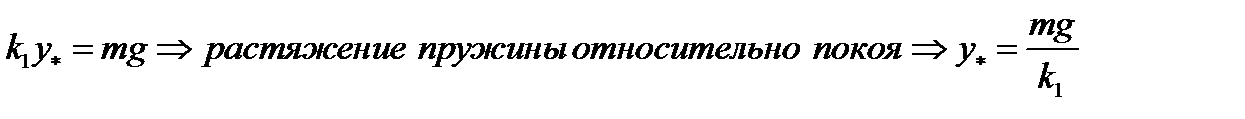
|
|
|
В момент времени 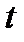 на пружину будет действовать сила упругости
на пружину будет действовать сила упругости 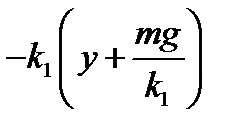 ,
,
сила сопротивления среды 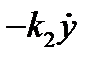 , внешняя сила воздействия на пружину
, внешняя сила воздействия на пружину 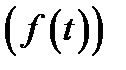 и сила тяжести
и сила тяжести 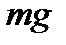 . По второму закону Ньютона
. По второму закону Ньютона
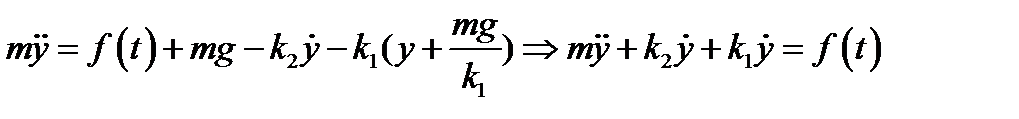
Получаем то же самое уравнение.
Рассмотрим различные ситуации.
Если на пружину не действует внешняя сила и она совершает колебания в среде с сопротивлением. То дифференциальное уравнение принимает вид 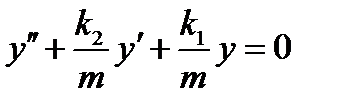 Положительная константа
Положительная константа 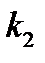 характеризует среду сопротивления движению. Положительная константа
характеризует среду сопротивления движению. Положительная константа 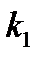 характеризует материал, из которого изготовлена пружина. Характеристическое уравнение даёт корни
характеризует материал, из которого изготовлена пружина. Характеристическое уравнение даёт корни
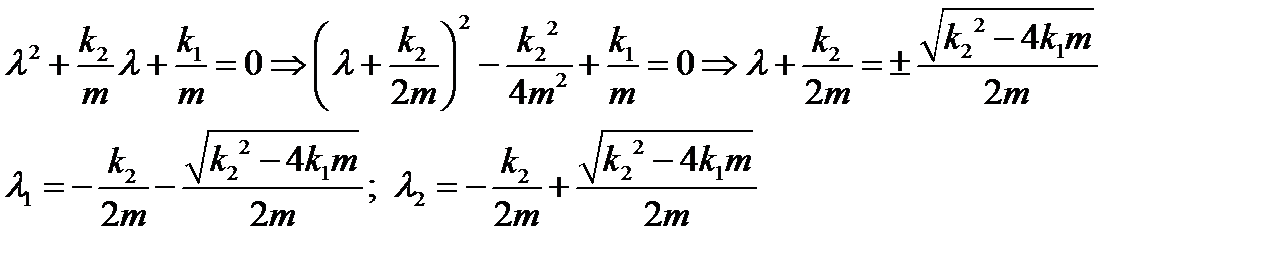
Решение неоднородного ЛДУ зависит от вида корней и правой части 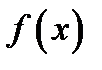 . На практике очень часто правая часть имеет специальный вид
. На практике очень часто правая часть имеет специальный вид 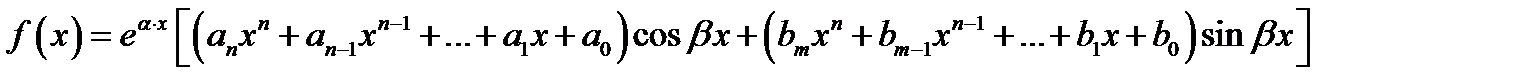
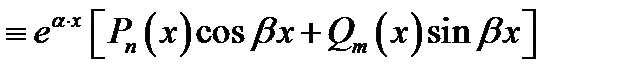 . (1)
. (1)
Определение 1. Назовём характерным числом правой части (1) комплексное число 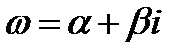 Вид решения неоднородного ЛДУ существенно зависит от того каким образом связаны между собойчисла
Вид решения неоднородного ЛДУ существенно зависит от того каким образом связаны между собойчисла 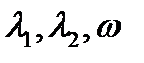 .
.
Рассмотрим примеры нахождения общего решения линейного неоднородного ОДУ с постоянными коэффициентами и правой частью специального вида. Данный алгоритм мы назвали методом подбора и рассматривали его на предыдущей лекции.
Пример 1. Найти общее решение неоднородного ЛДУ 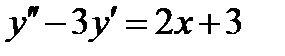 .
.
Решение. Находим корни 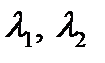 характеристического уравнения
характеристического уравнения 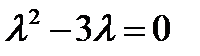 .
. 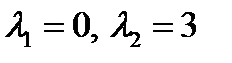 . Найденные
. Найденные 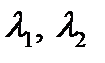 дают нам ФСР:
дают нам ФСР: 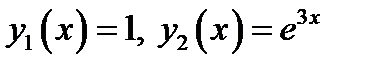 . Согласно теории линейных дифференциальных уравнений общее решение неоднородного уравнения задаётся формулой
. Согласно теории линейных дифференциальных уравнений общее решение неоднородного уравнения задаётся формулой
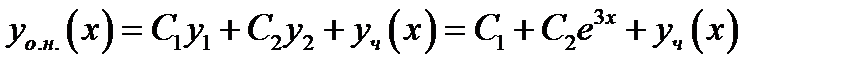 .Здесь
.Здесь 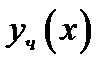 любое конкретное решение неоднородного уравнения. Выписываем характерное число
любое конкретное решение неоднородного уравнения. Выписываем характерное число 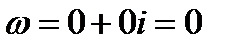 определяющее правую часть. Замечаем, что есть совпадение
определяющее правую часть. Замечаем, что есть совпадение 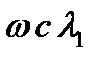 . Поэтому частное решение
. Поэтому частное решение 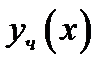 ищем в виде
ищем в виде 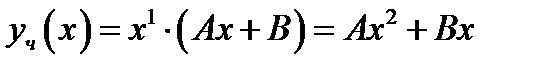 . Подберём
. Подберём 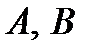 так, чтобы
так, чтобы 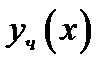 было решением
было решением 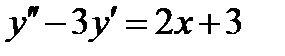 ,то есть
,то есть 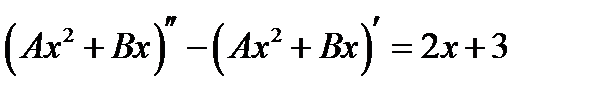 . Дифференцируя и раскрывая скобки получаем
. Дифференцируя и раскрывая скобки получаем 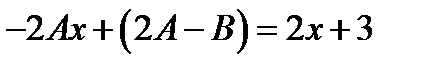 . Откуда
. Откуда 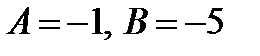 .
.
|
|
|
Общее решение имеет вид 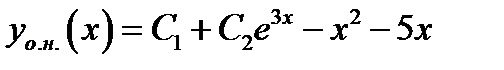 .
.
Пример 2. Найти общее решение неоднородного ЛДУ 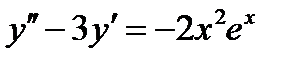 .
.
Решение. Находим корни 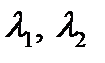 характеристического уравнения
характеристического уравнения 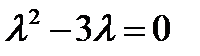 .
. 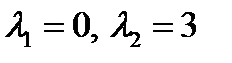 . Найденные
. Найденные 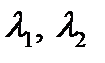 дают нам ФСР:
дают нам ФСР: 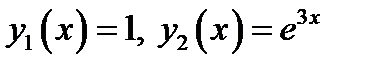 . Согласно теории линейных дифференциальных уравнений общее решение неоднородного уравнения задаётся формулой
. Согласно теории линейных дифференциальных уравнений общее решение неоднородного уравнения задаётся формулой
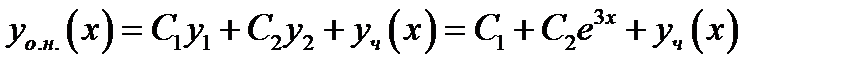 .Здесь
.Здесь 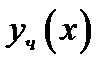 любое конкретное решение неоднородного уравнения. Выписываем характерное число
любое конкретное решение неоднородного уравнения. Выписываем характерное число 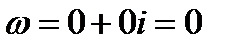 определяющее правую часть. Замечаем, что оба характеристических числа не совпадают с
определяющее правую часть. Замечаем, что оба характеристических числа не совпадают с 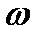 . Поэтому частное решение
. Поэтому частное решение 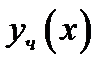 ищем в виде
ищем в виде 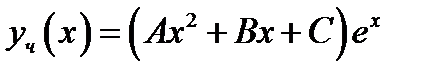 . Подберём
. Подберём 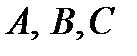 так, чтобы
так, чтобы 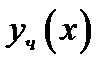 было решением
было решением 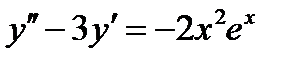 , то есть
, то есть 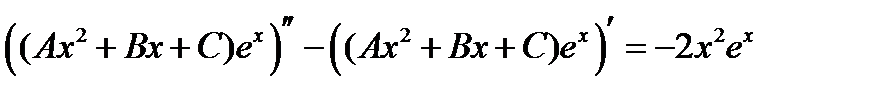 . Дифференцируя получаем
. Дифференцируя получаем
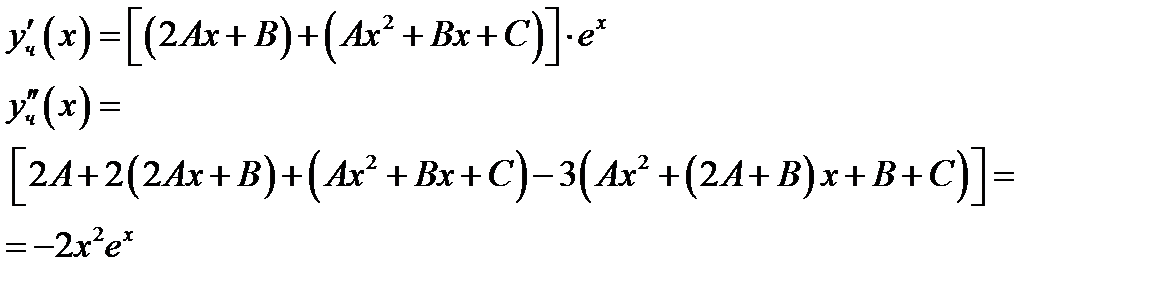
Раскрывая скобки, получаем 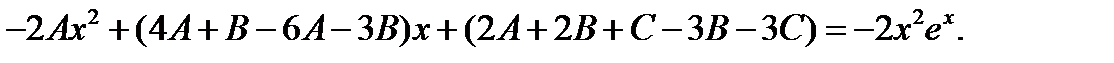
Отсюда 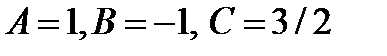 . Общее решение имеет вид
. Общее решение имеет вид 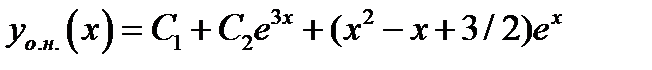 .
.
Пример 3. Найти общее решение неоднородного ЛДУ 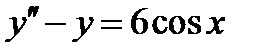 .
.
Решение. Находим корни 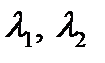 характеристического уравнения
характеристического уравнения 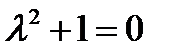 .
. 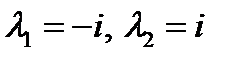 . Найденные
. Найденные 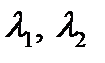 дают нам ФСР:
дают нам ФСР: 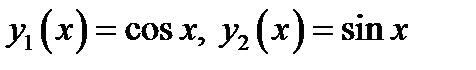 . Согласно теории линейных дифференциальных уравнений общее решение неоднородного уравнения задаётся формулой
. Согласно теории линейных дифференциальных уравнений общее решение неоднородного уравнения задаётся формулой
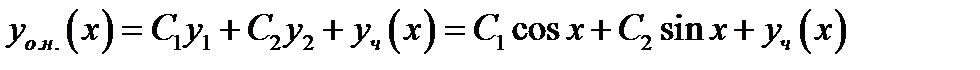 .Здесь
.Здесь 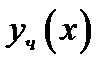 любое конкретное решение неоднородного уравнения. Выписываем характерное число
любое конкретное решение неоднородного уравнения. Выписываем характерное число 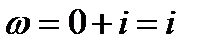 определяющее правую часть. Замечаем, что есть совпадение
определяющее правую часть. Замечаем, что есть совпадение 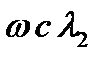 . Так как правая часть уравнения
. Так как правая часть уравнения 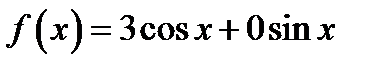 , то частное решение
, то частное решение 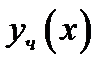 ищем в виде
ищем в виде 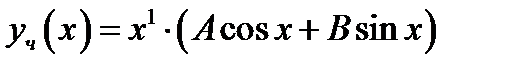 . Подберём
. Подберём 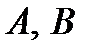 так, чтобы
так, чтобы 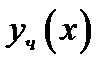 было решением
было решением 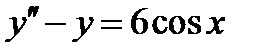 ,то есть
,то есть 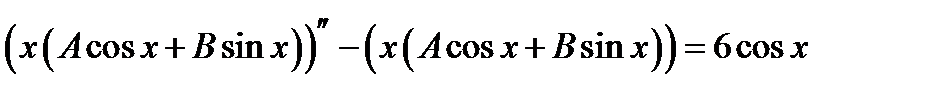 . Дифференцируя и раскрывая скобки получаем
. Дифференцируя и раскрывая скобки получаем 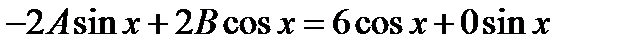 . Откуда
. Откуда 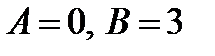 .
.
Общее решение имеет вид 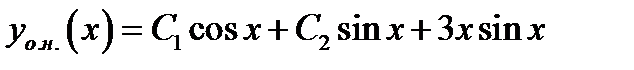 .
.
Вернёмся к задаче о пружинах. Как мы уже знаем уравнение колебания пружины имеет вид 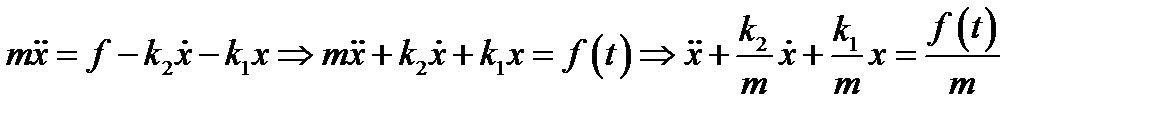
Или
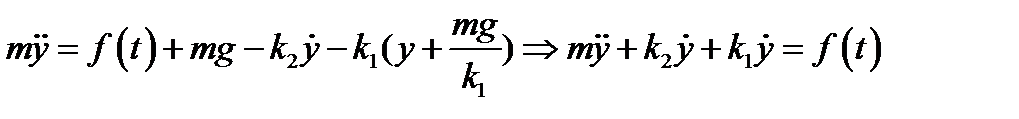
Пусть требуется решить задачу о колебании пружины, Если первоначальное отклонение от положения равновесия было равно 4м, а начальная скорость равнялась 0м/с. Таким образом требуется решить начальную задачу
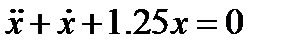
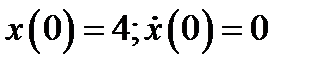
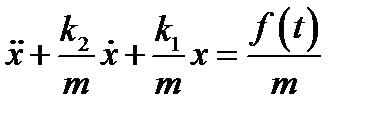
Тогда 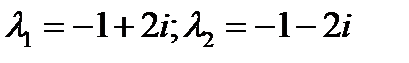 .Грузик на пружине будет совершать колебания по закону (общее решение)
.Грузик на пружине будет совершать колебания по закону (общее решение) 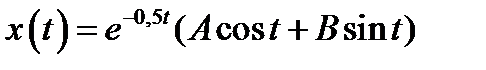 . Если первоначальное отклонение от положения равновесия было
. Если первоначальное отклонение от положения равновесия было 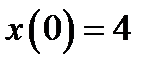 , а начальная скорость равнялась
, а начальная скорость равнялась 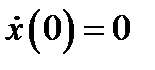 , то подставляя начальные данные в уравнение движения грузика определяем:
, то подставляя начальные данные в уравнение движения грузика определяем: 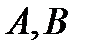 :
: 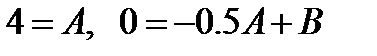 . Отсюда
. Отсюда
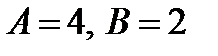 . Колебание грузика на пружине дается формулой:
. Колебание грузика на пружине дается формулой: 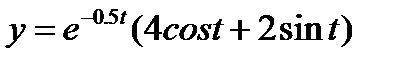
График движения представлен на рис.1.
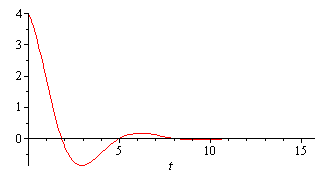
Рис.1
Уменьшим вязкость среды 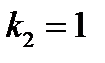 и положим
и положим 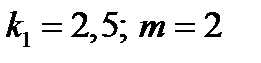 . Тогда колебания грузика будут даваться дифференциальным уравнением
. Тогда колебания грузика будут даваться дифференциальным уравнением 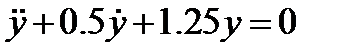 . Общее решение которого
. Общее решение которого
имеет вид 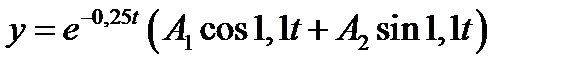
Если первоначальное отклонение от положения равновесия было 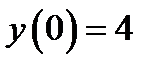 , а начальная скорость равнялась
, а начальная скорость равнялась 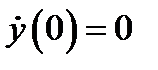 , то уравнение движения грузика будет
, то уравнение движения грузика будет
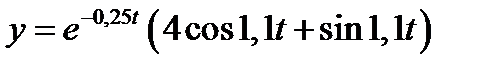
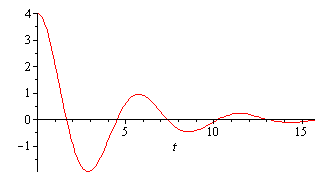
Рис.2
Пусть колебания грузика происходят в вакууме, т.е. среда не сопротивляется движению грузика 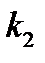 =0,
=0, 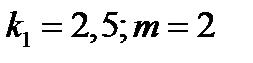 . Тогда дифференциальное уравнения движения грузика принимает вид
. Тогда дифференциальное уравнения движения грузика принимает вид
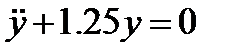 , а общее решение
, а общее решение 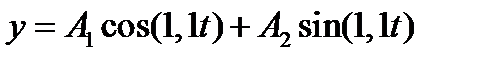 .
.
Если первоначальное отклонение от положения равновесия было 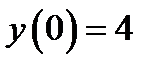 , а начальная скорость равнялась
, а начальная скорость равнялась 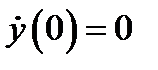 , то уравнение движения грузика будет
, то уравнение движения грузика будет 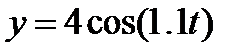
Рис.3
Пусть теперь среда, в которой колеблется пружина, очень вязкая 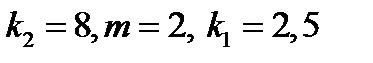
ДУ становится таким 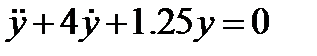 . А уравнения движения грузика имеет вид
. А уравнения движения грузика имеет вид 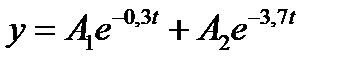
Если первоначальное отклонение от положения равновесия было 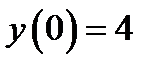 , а начальная скорость равнялась
, а начальная скорость равнялась 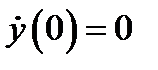 , то уравнение движения грузика будет
, то уравнение движения грузика будет
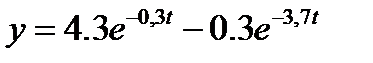

Рис.4
Пусть теперь среда, в которой колеблется пружина, такова, что 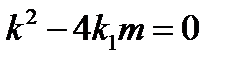 . Например
. Например
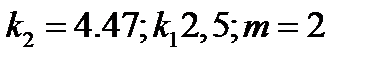 ДУ в этом случае становится таким
ДУ в этом случае становится таким 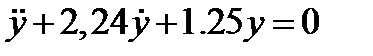 . А уравнение движения грузика имеет вид
. А уравнение движения грузика имеет вид 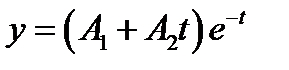 . Если первоначальное отклонение от положения равновесия было
. Если первоначальное отклонение от положения равновесия было 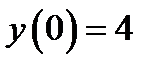 , а начальная скорость равнялась
, а начальная скорость равнялась 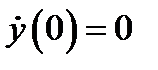 , то уравнение движения грузика будет
, то уравнение движения грузика будет 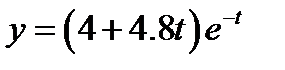
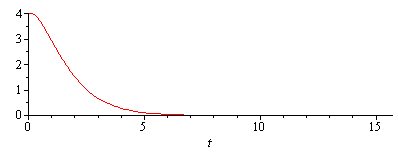
Рис.5
Движение грузика будет неустойчивым и если продолжать уменьшать вязкость среды начнутся колебания.
Рассмотрим движение грузика под действием внешней силы
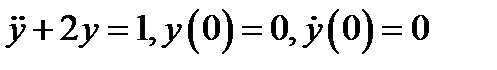
Центр колебаний груза смещён в точку 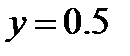
Рис.6
Рассмотрим движение грузика под действием внешней силы
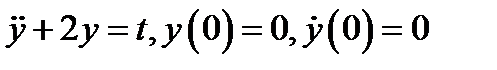
Рис.7
Центр колебаний груза постоянно с течением времени смещается вправо.
Рассмотрим движение грузика под действием внешней периодической силы
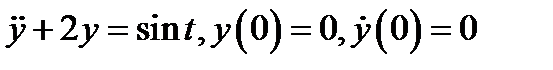
Рис.8
Рассмотрим движение грузика под действием внешней силы
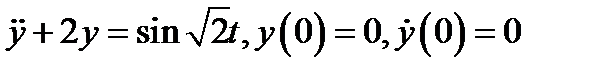
Рис 9. Амплитуда колебаний растёт (резонансное явление).
|
|
|
 2015-04-30
2015-04-30 557
557






