Найти общее решение неоднородной линейной системы
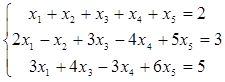
с помощью фундаментальной системы решений соответствующей однородной системы.
Решение.
Убедимся в том, что система совместна:
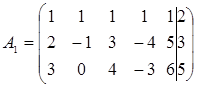 ~
~ 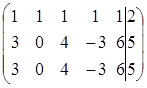 ~
~ 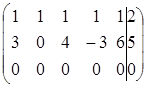 ~
~
~ 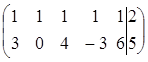 .
.
Итак, r (A) = r (A 1) = 2 – система совместна.
Составим по преобразованной матрице однородную систему:
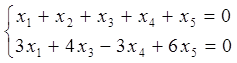
и найдем для нее фундаментальную систему решений:
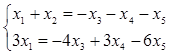 ,
,
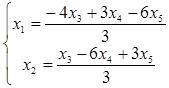 .
.
Фундаментальная система решений может быть выбрана так:
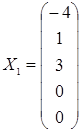 ,
,  ,
, 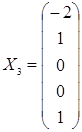 .
.
Теперь найдем какое-нибудь частное решение неоднородной системы
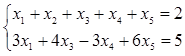 .
.
Положим х 3 = х 4 = х 5 = 0, тогда 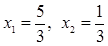 . Следовательно,
. Следовательно,
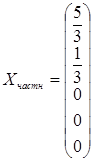 , и общее решение системы имеет вид:
, и общее решение системы имеет вид:
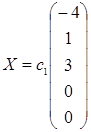
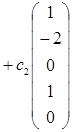
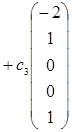
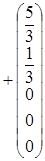 , где с 1, с 2, с 3 – произвольные постоянные.
, где с 1, с 2, с 3 – произвольные постоянные.
ТЕМА 1. Пределы функций
Для определения пределов последовательностей и функций используются некоторые известные приемы:
1. Если необходимо найти предел
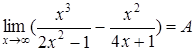 ,
,
можно предварительно привести к общему знаменателю
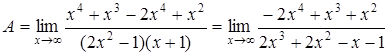 .
.
Поделив на член, имеющий максимальную степень, получим в числителе постоянную величину, а в знаменателе – все члены, стремящиеся к 0,то есть
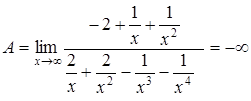 .
.
2. Аналогично, для примера 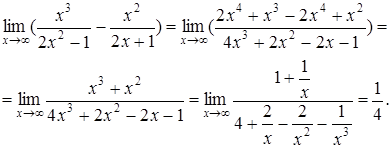
3. 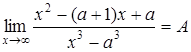 в этом пределе, если подставить x=a, то получится неопределенность, которую можно преодолеть, если разложить разность кубов в знаменателе
в этом пределе, если подставить x=a, то получится неопределенность, которую можно преодолеть, если разложить разность кубов в знаменателе 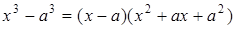 , а числитель в виде:
, а числитель в виде: 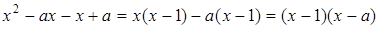 .
.
Тогда 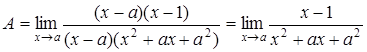 и подставив x=a, получим:
и подставив x=a, получим: 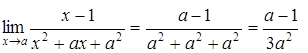 ;
;
4. 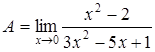 , при подстановке х=0, получим
, при подстановке х=0, получим 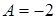 .
.
5. Однако, если необходимо найти предел рациональной функции
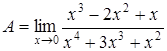 , то при делении на член с минимальной степенью, получим
, то при делении на член с минимальной степенью, получим
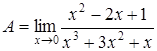 ; и, устремив х к 0, получим:
; и, устремив х к 0, получим: 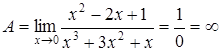
Если в пределах содержатся иррациональные выражения, то приходится вводить новые переменные для получения рационального выражения, или же переводить иррациональности из знаменателя в числитель и наоборот.
6. 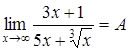 ; Сделаем замену переменной. Заменим
; Сделаем замену переменной. Заменим 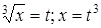 , при
, при 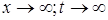 , получим
, получим 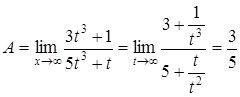 .
.
7. 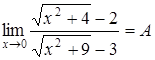 . Если числитель и знаменатель умножить на одно и то же число, то предел не изменится. Умножим числитель на
. Если числитель и знаменатель умножить на одно и то же число, то предел не изменится. Умножим числитель на 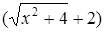 и разделим на это же выражение, чтобы предел не изменился, а знаменатель умножим на
и разделим на это же выражение, чтобы предел не изменился, а знаменатель умножим на 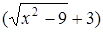 и разделим, на это же выражение. Тогда получим:
и разделим, на это же выражение. Тогда получим:
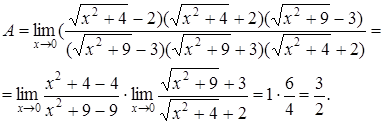
Для определения пределов часто используются замечательные пределы:
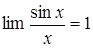 ; (1)
; (1)
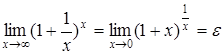 . (2)
. (2)
8. 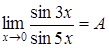 .
.
Для вычисления такого предела сведем его к 1-му замечательному пределу (1). Для этого умножим и разделим числитель на 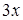 , а знаменатель на
, а знаменатель на 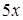 , тогда
, тогда 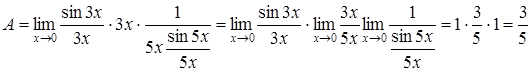 .
.
9. 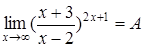 Для вычисления этого предела сведем его ко второму замечательному пределу. С этой целью из рационального выражения в скобках выделим целую часть и представим ее в виде правильной дроби. Так поступают в тех случаях, когда
Для вычисления этого предела сведем его ко второму замечательному пределу. С этой целью из рационального выражения в скобках выделим целую часть и представим ее в виде правильной дроби. Так поступают в тех случаях, когда 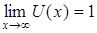 , где
, где 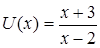 , а
, а 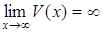 , где
, где 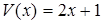 ;
;
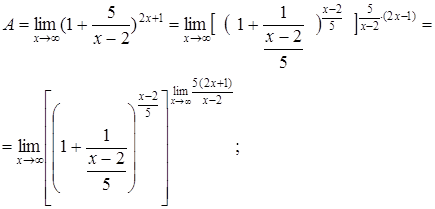
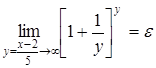 , а
, а 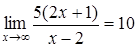 , то окончательно
, то окончательно 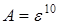 . Здесь использовалась непрерывность композиции непрерывных функций.
. Здесь использовалась непрерывность композиции непрерывных функций.
ТЕМА 2. Производная
Производной от функции 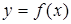 называется конечный предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю:
называется конечный предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю:
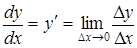 , или
, или 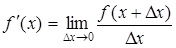 .
.
Геометрически производная представляет собой угловой коэффициент касательной к графику функции 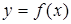 в точке х, то есть
в точке х, то есть 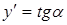 .
.
Производная есть скорость изменения функции в точке х.
Отыскание производной называется дифференцированием функции.
Формулы дифференцирования элементарных функций:
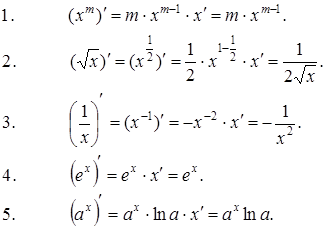
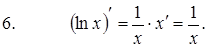
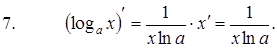
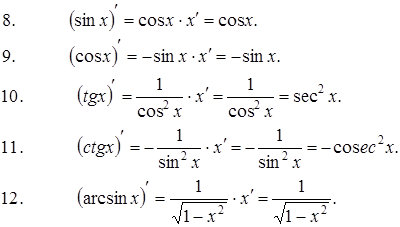
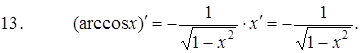

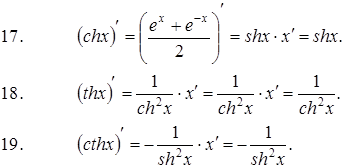 |
ТЕМА 3. Основные правила дифференцирования
Пусть 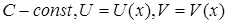 , тогда:
, тогда:
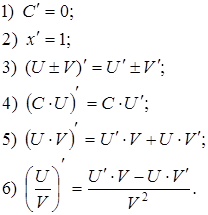
7) Если 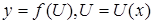 , то есть
, то есть  , где
, где 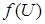 и
и 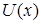 имеют производные, то
имеют производные, то 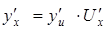 (правило дифференцирования сложной функции).
(правило дифференцирования сложной функции).
Примеры:
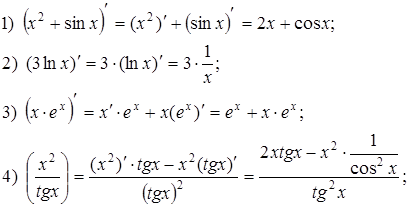
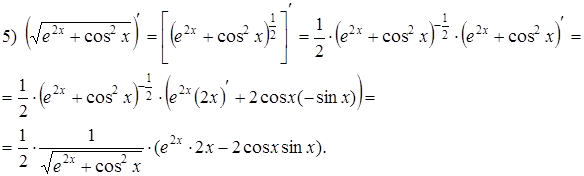
ТЕМА 4. Логарифмическое дифференцирование
Если требуется найти 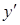 из уравнения
из уравнения 
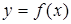 , то можно:
, то можно:
а) логарифмировать обе части уравнения
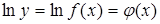 ;
;
б) дифференцировать обе части полученного равенства, где 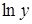 есть сложная функция от х,
есть сложная функция от х,
 .
.
в) заменить  его выражением через х
его выражением через х
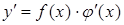 .
.
Пример: 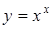
ТЕМА 5. Дифференцирование неявных функций
Пусть уравнение 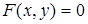 определяет
определяет  как неявную функцию от х.
как неявную функцию от х.
а) продифференцируем по х обе части уравнения 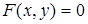 , получим уравнение первой степени относительно
, получим уравнение первой степени относительно 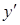 ;
;
б) из полученного уравнения выразим 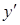 .
.
Пример: 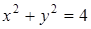 .
.
ТЕМА 6. Дифференцирование функций, заданных
 2015-05-14
2015-05-14 609
609








