Задание 2. Решение дифференциальных уравнений первого порядка с разделяющимися переменными

Лабораторная работа 9 (2008 г.)

Задание 1. Общее решение неоднородного дифференциального уравнения первого порядка.

Пример 1. Дано неоднородное дифференциальное уравнение
y^/ + 2xy = x· 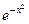·sin(x). Требуется найти общее решение уравнения.

Решение. Найдем решение для уравнения в общем виде y^/ = a(x)y + b(x) по готовой формуле.y(x, С):= С·exp(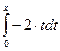) + )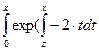·z·exp(-z²)·sin(z)dz y(x, С) → С·exp(-x²) + (sin(x) - x·cos(x))·exp(-x²).

Проверка.

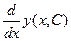+ 2·x·y(x, С) - x·exp(-x²)·sin(x) simplify → 0.

Задание 2. Решение дифференциальных уравнений первого порядка с разделяющимися переменными.

Пример 1. Решить дифференциальное уравнение: (1 + х²)y^/ = 2x .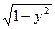

Решение. Запишем уравнение в нормальной форме: y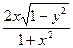^/ = . Получили уравнение с разделяющимися переменными. Разделим переменные, в результате получим уравнение вида: .

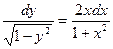Запишем выражение для общего интеграла этого уравнения:

F(x,y):= .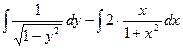

Вычислим выражение для общего интеграла данного уравнения:

F(x,y) → asin(y) – ln(1 + x²).

Общий интеграл уравнения записывается в виде F(x,y) = С:

asin(y) – ln(1 + x²) = С.

Общий интеграл описывает не все решения уравнения, а только те для которых у отличен от 1 и от -1. Все решения уравнения описываются равенствами:

asin(y) – ln(1 + x²) = С, y = 1, y = -1.

Выражение F(x,y) = С задает решение уравнения у = у(х) как функцию переменной х в неявной форме.

Проверка. Вычислим производную y^/(x) по формулам дифференцирования неявной функции и подставим ее в уравнение:

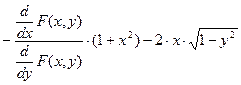simplify → 0.

После подстановки уравнение обратилось в тождество, следовательно, общий интеграл вычислен верно.