Последствия, симптомы и методика устранения ошибки спецификации эконометрической модели, состоящей во включении в линейное уравнение регрессии незначимой объясняющей переменной

Пусть на первом этапе экономист составил спецификацию модели множественной регрессии

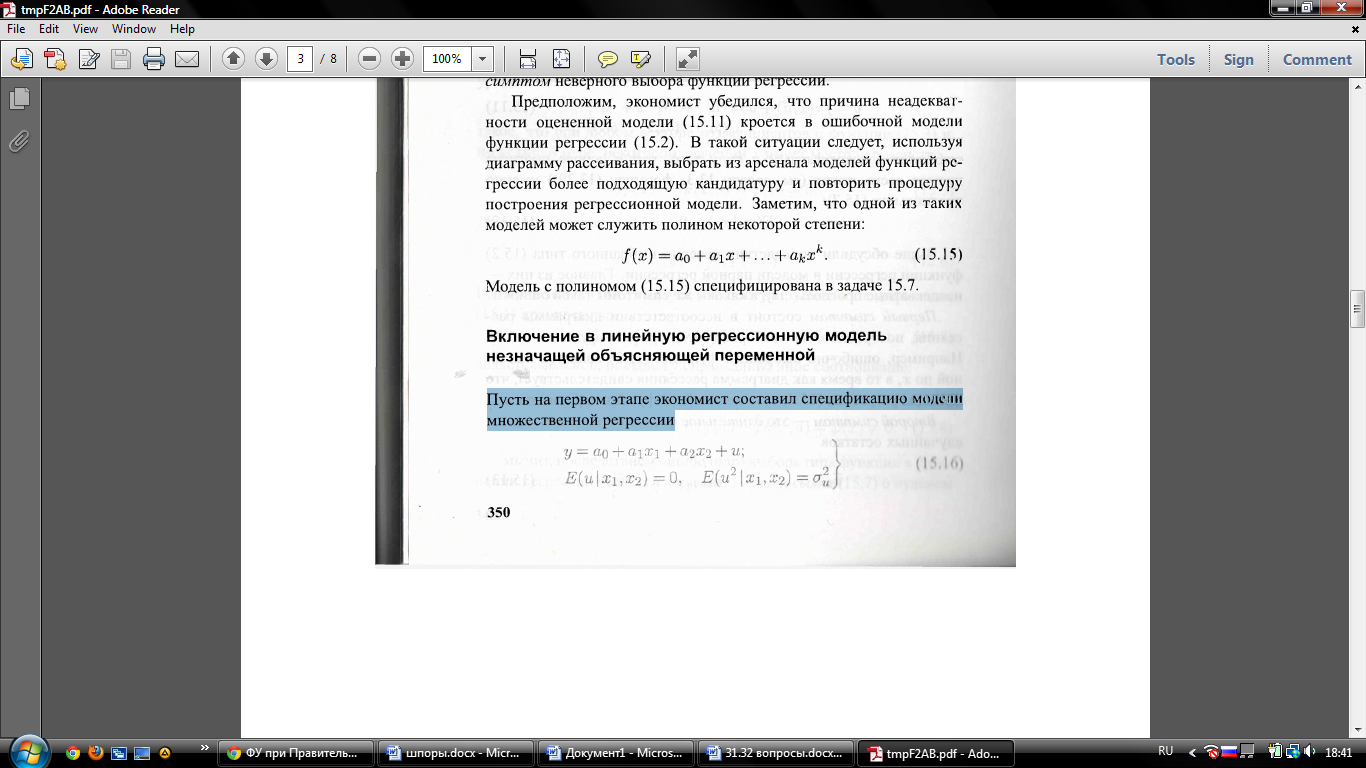
в ситуации, когда одна из объясняющих переменных, скажем, х₂, является лишней в том смысле, что справедлива гипотеза

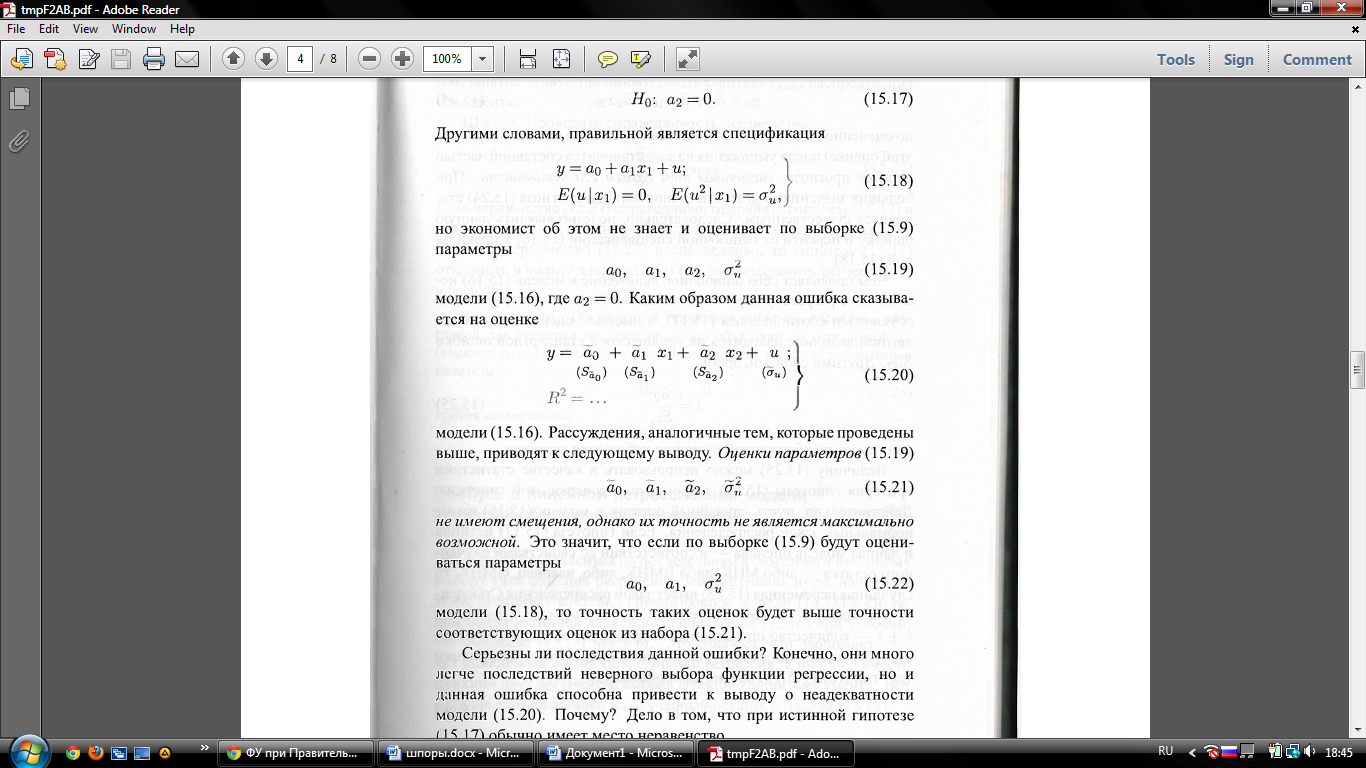
Другими словами, правильной является спецификация

но экономист об этом не знает и оценивает по выборке (15.9) параметры

модели (15.16), где а₂ = 0. Каким образом данная ошибка сказывается на оценке

модели (15.16). Рассуждения, аналогичные тем, которые проведены выше, приводят к следующему выводу. Оценки параметров (15.19)

не имеют смещения, однако их точность не является максимально возможной. Это значит, что если по выборке (15.9) будут оцениваться параметры

модели (15.18), то точность таких оценок будет выше точности соответствующих оценок из набора (15.21).

Серьезны ли последствия данной ошибки? Конечно, они много легче последствий неверного выбора функции регрессии, но и данная ошибка способна привести к выводу о неадекватности модели (15.20). Почему? Дело в том, что при истинной гипотезе (15.17) обычно имеет место неравенство

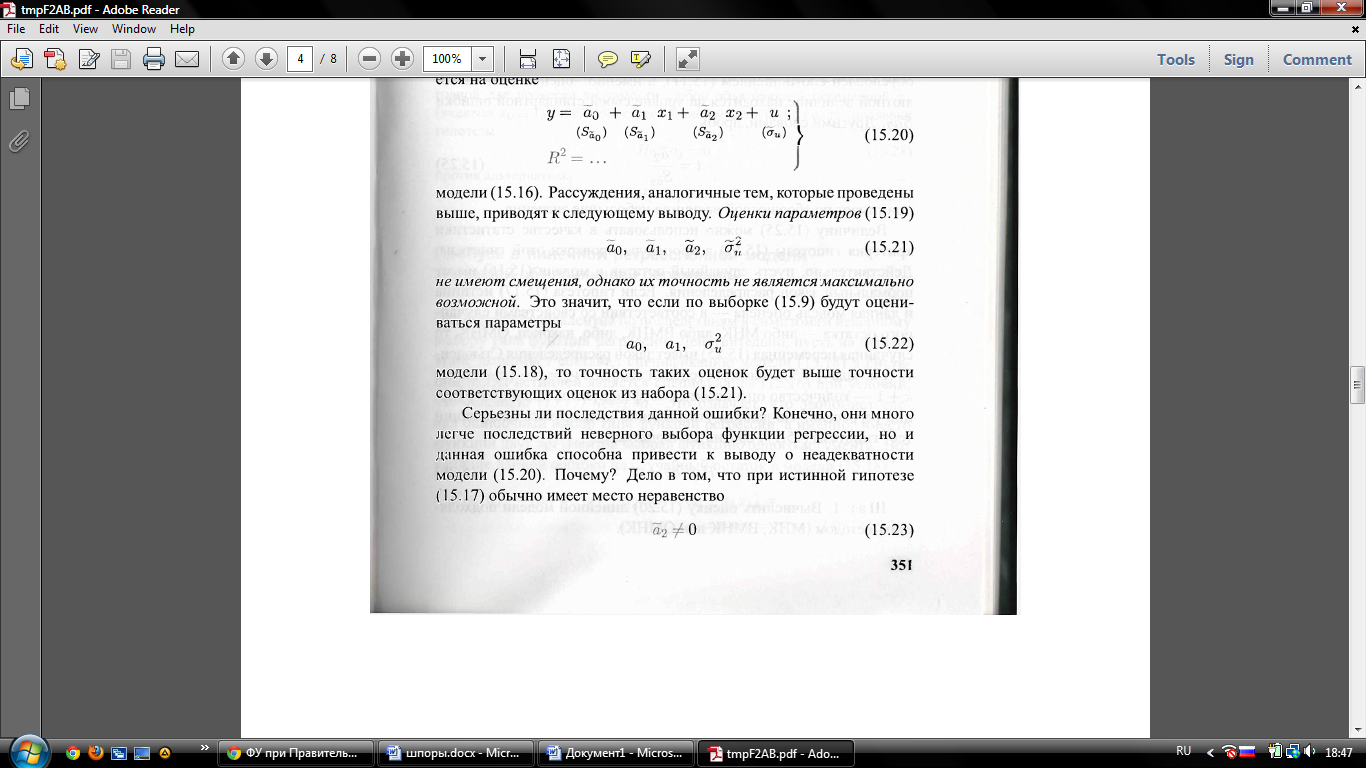
в силу отягощенности величины а₂ ошибкой оценивания Да2 = а₂ — а₂, в точности равной величине а₂. В прогнозе

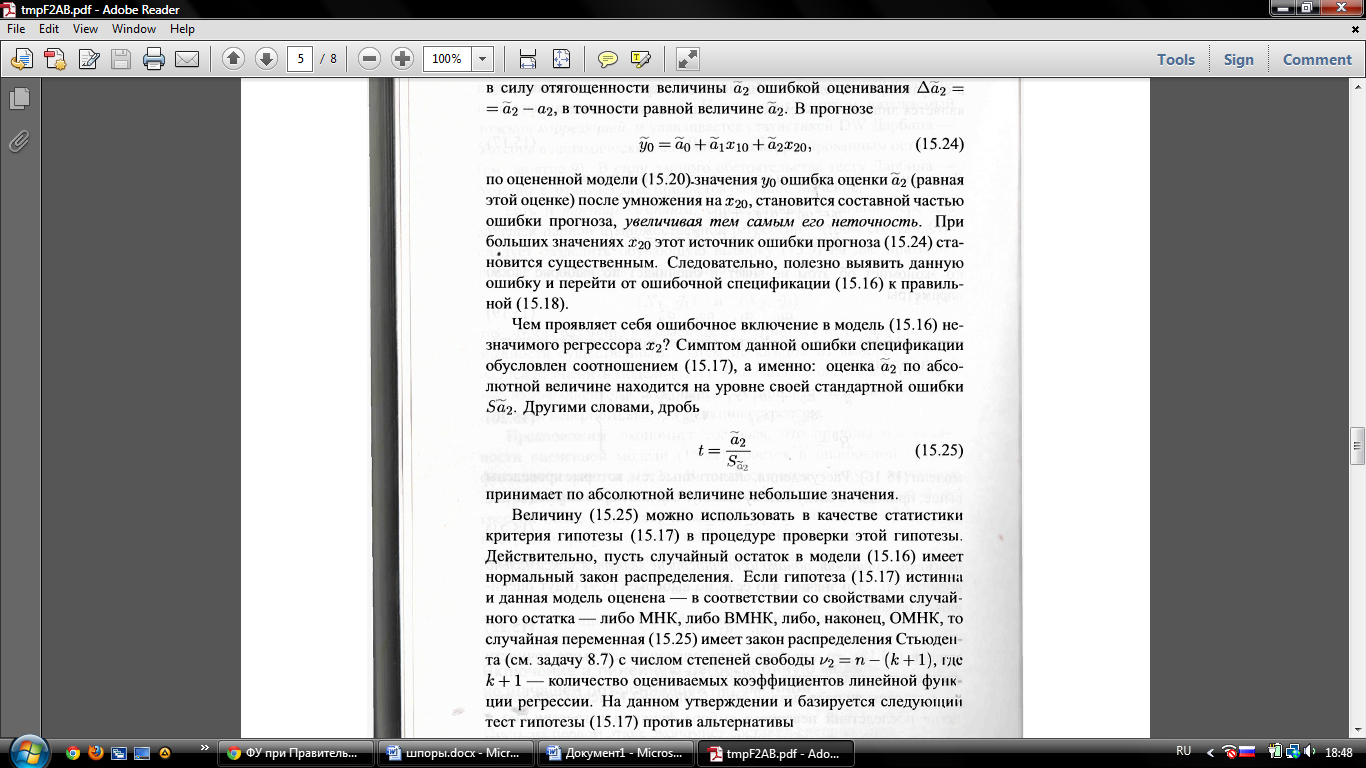
по оцененной модели (15.20).значения уо ошибка оценки а2 (равная этой оценке) после умножения на х2о, становится составной частью ошибки прогноза, увеличивая тем самым его неточность. При больших значениях ж2о этот источник ошибки прогноза (15.24) становится существенным. Следовательно, полезно выявить данную ошибку и перейти от ошибочной спецификации (15.16) к правильной (15.18).

Чем проявляет себя ошибочное включение в модель (15.16) незначимого регрессора х2? Симптом данной ошибки спецификации обусловлен соотношением (15.17), а именно: оценка а2 по абсолютной величине находится на уровне своей стандартной ошибки Sa2. Другими словами, дробь

принимает по абсолютной величине небольшие значения.

Величину (15.25) можно использовать в качестве статистики критерия гипотезы (15.17) в процедуре проверки этой гипотезы.

Действительно, пусть случайный остаток в модели (15.16) имеет нормальный закон распределения. Если гипотеза (15.17) истинна и данная модель оценена — в соответствии со свойствами случайного остатка — либо МНК, либо ВМНК, либо, наконец, ОМНК, то случайная переменная (15.25) имеет закон распределения Стьюдента (см. задачу 8.7) с числом степеней свободы z/2 = п — (к + 1), где к + 1 — количество оцениваемых коэффициентов линейной функции регрессии. На данном утверждении и базируется следующим тест гипотезы (15.17) против альтернативы

Шаг 1. Вычислить оценку (15.20) линейной модели подходящим методом (МНК, ВМНК или ОМНК).

Ш а г 2. Задаться доверительной вероятностью 1-α и по величинам αи v₂ рассчитать при помощи функции СТЬЮДРАСПОБР (см. занятие 7) двустороннюю (1-α) -квантиль t_крит распределения Стьюдента.

Ш а г 3. Проверить справедливость неравенства

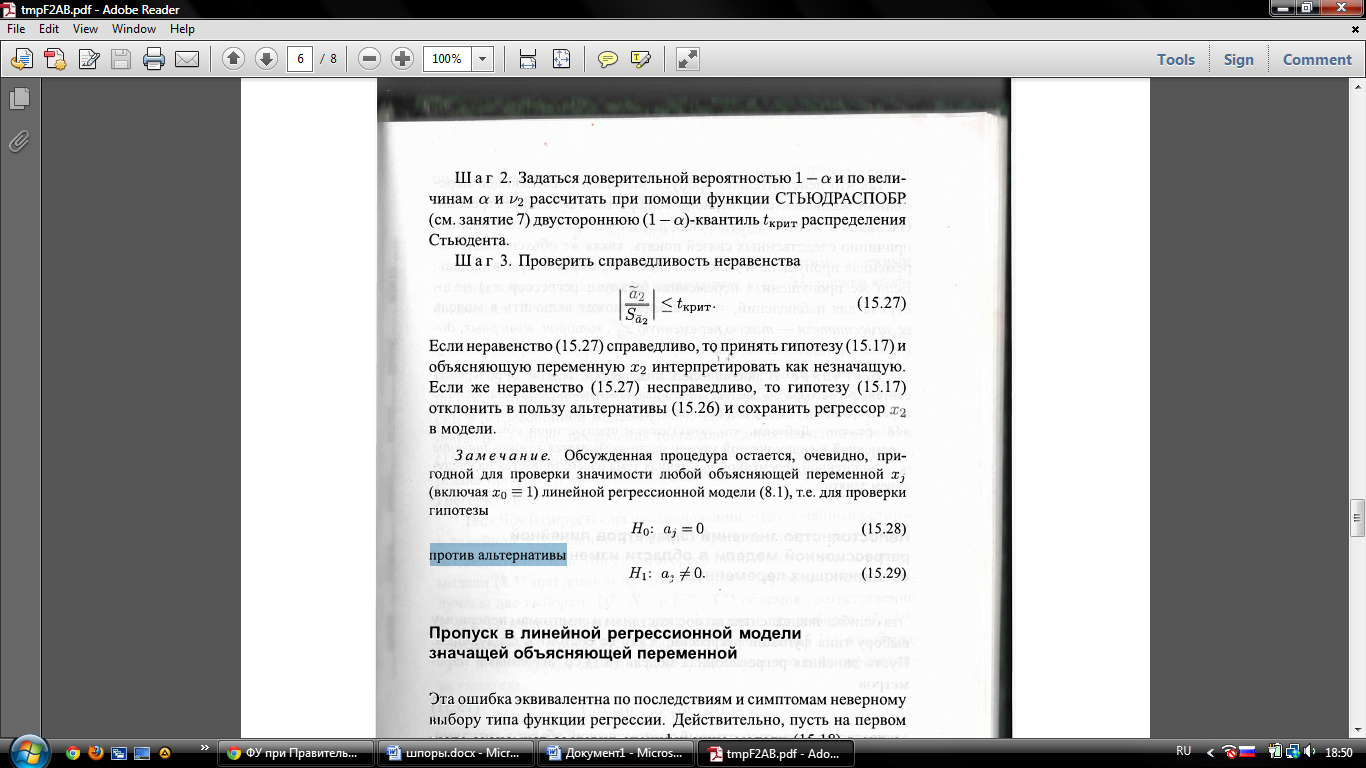
Если неравенство (15.27) справедливо, принять гипотезу (15.17) и объясняющую переменную х₂ интерпретировать как незначащую. Если же неравенство (15.27) несправедливо, то гипотезу (15.17) отклонить в пользу альтернативы (15.26) и сохранить регрессор в модели.

Замечание. Обсужденная процедура остается, очевидно, пригодной для проверки значимости любой объясняющей переменной Xj (включая х₀ = 1) линейной регрессионной модели (8.1), т.е. для проверки

гипотезы

против альтернативы