Качественная характеристика эластичности

] Если коэффициент эластичности по модулю меньше единицы, то говорят о неэластичности переменной y по x. Если коэффициент эластичности больше 1, то говорят, что y эластичен по x, так как каждый процент изменения фактора приводит к ещё большему изменению y. Если коэффициент эластичности равен 1, то говорят о единичной эластичности. В предельном случае, когда коэффициент эластичности равен бесконечности, говорят о совершенной эластичности. Соответственно, при нулевом коэффициенте эластичности — о совершенной неэластичности.

1. Регрессия.

зависимость среднего значения какой-либо случайной величины от нек-рой другой величины или от нескольких величин. Если, например, при каждом значении х=x_i наблюдается n_i значений случайной величины Y, то зависимость средних арифметических

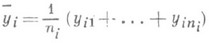
этих значений от x_i и является Р. в статистич. понимании этого термина. При обнаруженной закономерности изменения 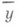с изменением хпредполагается, что в основе наблюдаемого явления лежит вероятностная зависимость: при каждом фиксированном значении хслучайная величина Y имеет определенное распределение вероятностей с математич. ожиданием, к-рое является функцией х: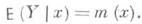

Зависимость 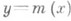, где хиграет роль "независимой" переменной, наз. р е г р е с с и е й (или ф у н к ц ие й р е г р е с с и и) в вероятностном понимании этого термина. График функции т(х)наз. л и н и е й р ег р е с с и и, или к р и в о й р е г р е с с и и, величины Y по х. Переменная хназ. р е г р е с с и о н н о й п е р е м е н н о й, или р е г р е с с о р о м. Точность, с к-рой линия регрессии Yпо хпередает изменение Yв среднем при изменении х, измеряется дисперсией величины Y, вычисляемой для каждого значения х:

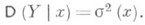
Графически зависимость дисперсии s² (х)от хвыражается т. н. с к е д а с т и ч е с к о й л и н и е й. Если s²(х)=0при всех значениях x, то с вероятностью 1 величины связаны строгой функциональной зависимостью. Если s² (х)№0ни при каком значении хи т (х)не зависит от х, то регрессия Yпо хотсутствует..

В теории вероятностей задача Р. решается применительно к такой ситуации, когда значения регрессионной переменной х соответствуют значениям нек-рой случайной величины Xи предполагается известным совместное распределение вероятностей величин Xи Y(при этом математич. ожидание 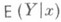и дисперсия 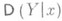будут соответственно условным математич. ожиданием и условной дисперсией случайной величины Yпри фиксированном значении X=x). В этом случае определены две Р.: Y по х и X по у, и понятие Р. может быть использовано также для того, чтобы ввести нек-рые меры взаимосвязанности случайных величин X и Y, определяемые как характеристики степени концентрации распределения около линий Р. (см. Корреляция).

Функции Р. обладают тем свойством, что среди всех действительных функций f(x)минимум математич. ожидания 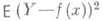достигается для функции f(x) = т (х), то есть регрессия Y по хдает наилучшее (в указанном смысле) представление величины Y. Наиболее важным является тот случай, когда регрессия Y по хл и н е й н а, т. е.

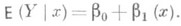
Коэффициенты b₀ и b₁, наз. коэффициентами Р., легко вычисляются:

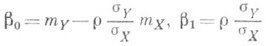
(здесь r - корреляции коэффициент X и Y, ,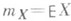

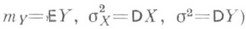, и п р я м а я регрессии Y по х имеет вид

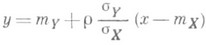
(аналогичным образом находится прямая регрессии Xпо у). Точная линейная Р. имеет место в случае, когда двумерное распределение величин Xи Y является нормальным.

В условиях статистич. приложений, когда для точного определения Р. нет достаточных сведений о форме совместного распределения вероятностей, возникает задача приближенного нахождения Р. Решению этой задачи может служить выбор из всех функций g(x), принадлежащих заданному классу, такой функции, к-рая дает наилучшее представление величины Y в том смысле, что минимизирует математич. ожидание 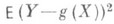. Найденная функция наз. с р е д н е й к в а д р а т и ч е с к о й Р.

Простейшим будет случай л и н е й н о й с р е д н е й к в а д р а т и ч е с к о й Р., когда отыскивают наилучшую линейную аппроксимацию величины Y посредством величины X, т. е. такую линейную функцию

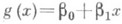, для к-рой выражение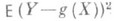

принимает наименьшее возможное значение. Данная экстремальная задача имеет единственное решение

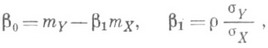
т. е. вычисление приближенной линии Р. приводит к тому же результату, к-рый получен в случае точной линейной Р.:

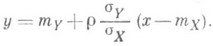
Минимальное значение 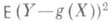при вычисленных значениях параметров равно 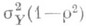. Если регрессия т(х)существует, то при любых b₀ и b₁ имеет место соотношение

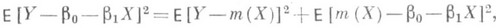
откуда следует, что прямая средней квадратич. регрессии 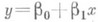дает наилучшее приближение к линии регрессии т(х), если измерять расстояние вдоль оси у. Поэтому если линия т(х)есть прямая, то она совпадает с прямой средней квадратической Р.

В общем случае, когда Р. сильно отличается от линейной, можно поставить задачу нахождения многочлена 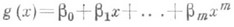нек-рой степени т, для к-рого среднее значение 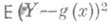имеет возможно меньшее значение.

Такое решение задачи соответствует п а р а б о л ич е с к о й (или п о л и н о м и а л ь н о й) средней квадратической Р. (см. Параболическая регрессия).порядка т. Кривая 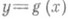есть парабола m-го порядка, дающая наилучшую аппроксимацию истинной линии Р. Обобщением параболической Р. служит функция Р., выраженная линейной комбинацией тех или иных заданных функций:

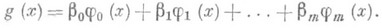
Наиболее важное значение имеет случай, когда j₀ (х), ..., j _m (х) - ортогональные многочлены соответствующих порядков, построенные по распределению X. Другими примерами н е л и н е й н о й (к р и в о л ин е й н о й) Р. являются случаи тригонометрической Р., показательной Р., и т. п.

Понятие Р. естественным образом обобщается на тот случай, когда вместо одной регрессионной переменной рассматривается нек-рое множество переменных. Если случайные величины X₁ Х ₂, ..., Х _пимеют совместное распределение вероятностей, то множественная Р. определяется, напр., как регрессия X₁ по x₂ ,..., х _п:

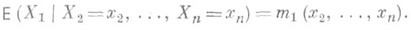
Соответствующее уравнение определяет поверхность регрессии Х ₁ по х ₂ ,..., х _n. Линейная регрессия Х ₁по х ₂ ,..., х _п имеет вид

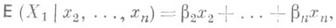
где b₂,..., b _n - коэффициенты Р. (при 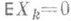). Линейная средняя квадратическая Р. величины Х ₁ по x₂,..., х _п определяется как наилучшая линейная оценка величины Х ₁ величинами Х ₂ ,..., Х _п в смысле обращения в минимум выражения

Соответствующая п л о с к о с т ь Р. дает наилучшую аппроксимацию поверхности регрессии x₁=m(x₂,..., х_п), если последняя существует. Если поверхность Р. есть плоскость, то она необходимо совпадает с плоскостью средней квадратической Р. (так будет в случае, когда совместное распределение всех пвеличин нормально).

Простым примером регрессии Yпо Xявляется зависимость между Yи X, к-рая выражается соотношением 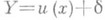, где 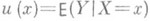, а случайные величины Xи dнезависимы. Это представление полезно, когда планируется эксперимент для изучения функциональной связи у=и (х)между неслучайными величинами уи х. Эта же модель Р. используется во многих приложениях при изучении характера зависимости случайной величины Yот неслучайной величины х. На практике выбор функции у=и (х)и оценку неизвестных коэффициентов Р. по экспериментальным данным производят методами регрессионного анализа.

1. Динамичное программирование.

раздел математики, посвященный теории и методам решения многошаговых задач оптимального управления.

В Д. п. для управляемых процессов среди всевозможных управлений ищется то, к-рое доставляет экстремальное (наименьшее или наибольшее) значение целевой функции - нек-рой числовой характеристики процесса. Под многошаговостью понимают либо многоступенчатую структуру процесса, либо что управление разбивается на ряд последовательных этапов (шагов), соответствующих, как правило, различным моментам времени. В ряде задач многошаговость проистекает из существа процесса (напр., в задаче определения оптимальных размеров ступеней многоступенчатой ракеты или при нахождении наиболее экономичного режима полета самолетов), но она может вводиться искусственно для того, чтобы обеспечить возможность применения метода Д. п. Таким образом, в названии Д. п. под программированием понимают принятие решений, планирование, а слово динамическое указывает на существенную роль времени и порядка выполнения операций в рассматриваемых процессах и методах.

Методы Д. п. являются составной частью методов, используемых в исследовании операций, и применяются в задачах оптимального планирования (напр., в задачах об оптимальных распределениях ресурсов, в теории управления запасами, в задачах замены оборудования и т. д.) и при решении многих технических проблем (напр., в задачах управления последовательными химическими процессами, в задачах оптимального проектирования прокладки дорог и др.).

Проиллюстрируем основную идею. Пусть процесс управления нек-рой системой Xсостоит из тшагов (этапов); на i-м шаге управление y_i переводит систему из состояния x_{i- 1}, достигнутого в результате (i-1)-го шага, в новое состояние ж,-. Этот процесс перехода осуществляет заданная функция f_i (x, у), и новое состояние определяется значениями x_{i- 1}, y_i:

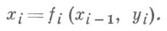
Таким образом, управления у ₁, у ₂,..., у _т переводят систему из начального состояния 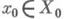в конечное - 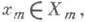где Х ₀ и Х _т - совокупности допустимых начальных и конечных состояний системы X. Опишем одну из возможных постановок экстремальной задачи. Начальное состояние х ₀ задано. Требуется выбрать управления у ₁, у ₂,..., у _т таким образом, чтобы система Xперешла в допустимое конечное состояние и при этом заданная целевая функция F(x₀, у ₁,x₁, у ₂,..., у _т, х _т)достигла максимального значения F*, т. е.

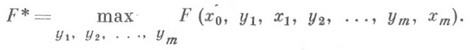
Важной особенностью метода Д. п. является то, что он применим лишь для аддитивной целевой функции.. В рассмотренном примере это означает, что

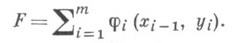
Кроме того, в методе Д. п. требуется, чтобы задача характеризовалась отсутствием "последействия": решения (управления), принимаемые на шаге, оказывают влияние только на состояние х _i системы в момент i. Другими словами, процессы, описываемые функциями вида 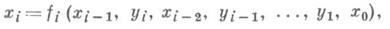не рассматриваются. Оба упомянутых ограничительных условия можно ослабить, но только за счет существенного усложнения метода.

Для решения задач Д. п. обычные методы математического анализа либо вообще неприменимы, либо приводят к огромному числу вычислений. В основе метода Д. п. лежит принцип оптимальности, сформулированный Р. Беллманом (R. Bellman): предположим, что осуществляя управление дискретной системой X, мы уже выбрали некоторые управления дискретной системой у ₁, у ₂,..., у _k тем самым траекторию состояний х ₀, х ₁,..., x_k, и хотим завершить процесс, т. е. выбрать y_{k+ 1}, y_k+2,..., у _т (а значит и x_{k+ 1},x_{k+ 2},...,x_m);тогда, если завершающая часть процесса не будет оптимальной в смысле достижения максимума функции

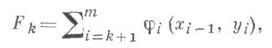
то и весь процесс не будет оптимальным.

Пользуясь принципом оптимальности, легко получить основное функциональное соотношение. Определим последовательность функций переменной х:

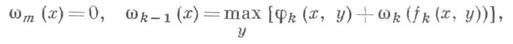
k=1,2,..., т. Здесь максимум берется по всем управлениям, допустимым на шаге к. Соотношение, определяющее зависимость w_k-1 от w_k, принято называть Беллмана уравнением. Смысл функций w_k-1 (х).нагляден: если система на шаге k-1 оказалась в состоянии х, то w_k-1(x) есть максимально возможное значение функции F. Одновременно с построением функций w_k-1 (х). находятся условные оптимальные управления y_k (х)на каждом шаге (т. е. значения оптимального управления при всевозможных предположениях о состоянии хсистемы на шаге k-1). Окончательно оптимальные управления находятся последовательным вычислением величин

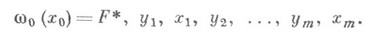
Из сказанного очевидна следующая особенность метода Д. п.- с его помощью решается не одна конкретная задача при определенном х ₀, а сразу все подобные однотипные задачи при любом начальном состоянии. Поскольку численная реализация метода Д. п. весьма сложна, т. к. требует большого объема памяти ЭВМ, то его целесообразно применять в тех случаях, когда необходимо многократно решать типовые задачи (скажем, определение оптимального режима полета самолета при меняющихся погодных условиях). Несмотря на то, что задача Д. п. формулируется для дискретных процессов, в ряде случаев метод Д. п. с успехом применяется для решения динамических задач с непрерывными параметрами.

Д. п. дало новый подход ко многим задачам вариационного исчисления..

Важным разделом Д. п. являются стохастические задачи Д. п.- задачи, в к-рых на состояние системы и на целевую функцию влияют случайные факторы. К таким задачам относятся, напр., задачи оптимального регулирования запасов с учетом возможностей случайного пополнения запасов. Здесь наиболее естественной областью применения Д. п. являются управляемые марковские процессы.

Метод Д. п. был предложен Р. Беллманом. Строгое обоснование метода Д. п. было получено в результате работ Л. С. Понтрягина и его учеников по математической теории управляемых процессов (см. Оптимального управления математическая теория).

Хотя метод Д. п. существенно упрощает исходные задачи, однако явное его применение, как правило, весьма громоздко. Для преодоления этих трудностей разрабатываются приближенные методы Д. п.

1. Однофакторная линейная регрессия.

Однофакторная линейная регрессия – регрессионная зависимость между двумя переменными у и х (модель) вида

у=b₀+b₁x+e,

где у – отклик, х – фактор, е – аддитивная помеха, величина, учитывающая случайные ошибки измерений, случайные шумы, влияние неучтенных факторов. При определении уравнения регрессии целесообразно принять условие, что математическое ожидание аддитивной помехи равно нулю: М(е)=0. В этом случае уравнение регрессии будет иметь вид у=b₀+b₁x.

1. Гармонический анализ.

ГАРМОНИЧЕСКИЙ АНАЛИЗ

название раздела математики и математич. метода. В Г. а. как раздел математики обычно включают: теорию тригонометрических рядов (одномерных и многомерных), Фурье преобразований (функций одного и нескольких переменных), почти периодических функций, Дирихле рядов, приближения теорию (функций тригонометрическими полиномами), гармонический анализ абстрактный и нек-рые другие математич. дисциплины, близкие к указанным. Метод заключается в сведении нек-рых задач (из различных областей математики) к вопросам Г. а. и решаемых на его основе. Напр.: теория функций комплексного переменного в вопросах граничного поведения аналитических в единичном круге функций, по существу, сливается с теорией тригонометрич. рядов; изучение свойств случайных величин при помощи харак-теристич. функций - применение метода Г. а. в теории вероятностей; нек-рые объекты функционального анализа тесно связаны с тригонометрич. рядами, почти периодич. функциями и др. объектами Г. а.; в теории дифференциальных уравнений при помощи относящегося к Г. а. Фурье метода находятся решения различных уравнений математич. физики; наконец, многочисленные прикладные задачи вычислительной математики решаются на основе применения рядов и интегралов Фурье - объектов Г. а. Е. м. Никитин.

1. Тригонометрическая интерполяция.

Интерполяция - приблежение одной функции с помощью другой. Это может понадобиться в случае, когда вычислительно сложную функцию нужно заменить более легкой. Есть много видов метода интерполяции и способов их применения. Здесть мы рассмотрим особый вид интерполяции - тригонометрическую. На класс функций, при которых ее удобно использовать накладывается сильное ограничение - они должны быть периодическими, но более подробно об этом ниже.

Для использования математических формул для тригонометрической интерполяцией необходимо ознакомиться с теорией дискретного преобразования Фурье.