Оценка средней относительной ошибки для каждой модели

Добавим в исходную таблицу столбцы «Теоретические» и «погрешность».

а) Линейная модель:

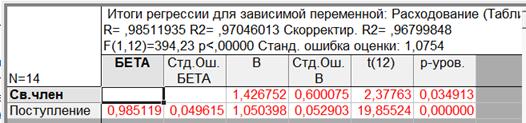
Рисунок 1.11– Результаты линейной регрессии

В столбце «Теоретические» зададим формулу 1,42675+1,0504*v1,

В столбце «Погрешность» – формулу: =abs((v2-v3)/v2).

В столбец «Погрешность» – формулу: abs(v2–v3)

В столбец % – формулу =v4/v2*100. В результате получим таблицу:

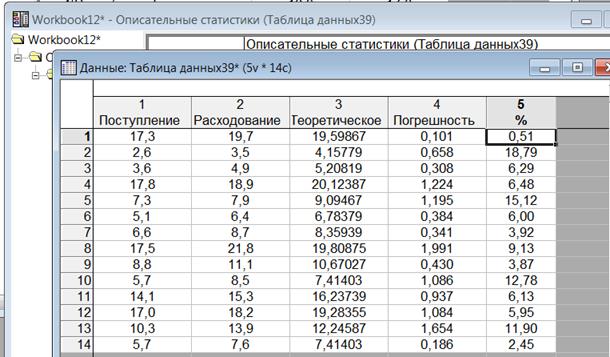
Рисунок 1.12 – К вычислению средней погрешности для линейной регрессии

Далее выполняем команду «Анализ → Описательные статистики и таблицы → Описательные статистики. Определим переменные Погрешность и %. На закладке «Дополнительно» оставим флажок только для среднего значения

Рисунок 8.3 – Нахождение средней ошибки линейной регрессии

Итак. Оценка линейного уравнения регрессии показывает:

1) F(1,7) = 5,2119 и имеет уровень 0,05639;

2) Для параметра b получили уровень значимости 0,0349. Это значит, что b незначительно отличается от нуля.

3) Средняя ошибка составляет 0,827, или 7,8% от среднего значения, что вполне удовлетворительно. Вывод: линейное уравнение

Расходование = 1,42675+1,0504*Поступление

является применимым для описания зависимости между расходованием и поступлением.

б) Квадратичная модель.

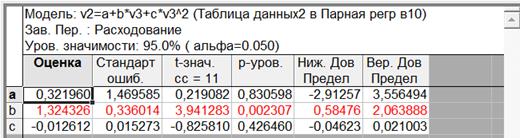
Рисунок 1.13– Результаты квадратичной регрессии

В столбце основной таблицы «Теоретические» зададим формулу

=0,32196+1,32433*v1–0,01261*v1^2.

В столбец «Погрешность» – формулу: abs(v2–v3)

В столбец % – формулу =v4/v2*100. В результате получим таблицу:

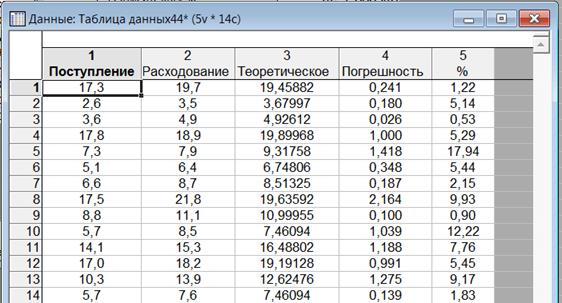
Рисунок 1.14 – К вычислению средней ошибки квадратичной регрессии

Далее выполняем команду «Анализ → Описательные статистики и таблицы → Описательные статистики. Определим переменные Погрешность и %. На закладке «Дополнительно» оставим флажок только для среднего значения

Рисунок 1.15 – Нахождение средней ошибки квадратичной регрессии

Итак. Оценка квадратичного уравнения регрессии показывает:

2) Для параметра a получили уровень значимости 0,8306. Это значит, что a незначительно отличается от нуля.

2) Для параметра b получили уровень значимости 0,002307. Это значит, что b значительно отличается от нуля.

2) Для параметра c получили уровень значимости 0,42646. Это значит, что c незначительно отличается от нуля.

3) Средняя ошибка составляет 0,7355, или 6,07%, что является удовлетворительным показателем.

Вывод: квадратичная модель:

Расходование = 0,321960,32196*Поступление–0,01261*Поступление²

применима для описания зависимости между Поступлением и расходованием.

в) Экспоненциальная функция y = ae^bx:

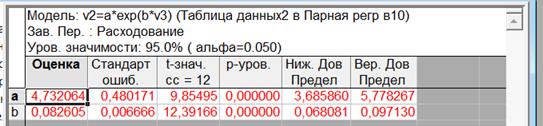
Рисунок 1.15– Результаты экспоненциальной регрессии

Уравнение регрессии: y = 4,732064·e^0,082605x

Множитель a значим на уровне α =0,05: p-уровень = 0,0000 < 0,05

Коэффициент b значим: p-уровень = 0,0000 < 0,05

В столбце «Теоретические» зададим формулу =4,732064*exp(0,082605*v1).

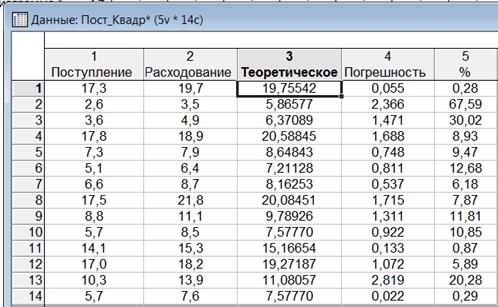
Рисунок 1.15 – К вычислению средней ошибки экспоненциальной регрессии

Далее выполняем команду «Анализ → Описательные статистики и таблицы → Описательные статистики. Определим переменную Погрешность и %. На закладке «Дополнительно» оставим флажок только для среднего значения

Рисунок 1.16 – Нахождение средней ошибки экспоненциальной регрессии

Итак, оценка экспоненциального уравнения регрессии показывает:

Средняя ошибка составляет 1,11952, или 13,787% от среднего значения, что не применимо для описания зависимости между расходованием и поступлением.

Вывод: экспоненциальное уравнение

Расходование = 4,732064·e^{0,082605 Поступление} применимо для описания зависимости между поступлением и расходованием.

г) Степенная функция y = ax^b:

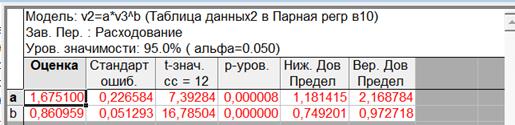
Рис. 1.17– Результаты степенной регрессии

Уравнение регрессии: y = 1,6751·x^0,860959

Множитель a значим на уровне α =0,05: p-уровень = 0,000008 < 0,05

Коэффициент b значим: p-уровень = 0,0000 < 0,05

В столбце «Теоретические» зададим формулу =1,6751*v1^0,860959.

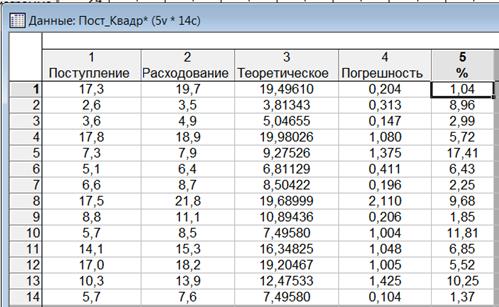
Рис. 1.18 – К вычислению средней ошибки степенной регрессии

Далее выполняем команду «Анализ → Описательные статистики и таблицы → Описательные статистики. Определим переменную Погрешность и %. На закладке «Дополнительно» оставим флажок только для среднего значения

Рисунок 1.19 – Нахождение средней ошибки степенной регрессии

Итак, оценка степенной регрессии показывает, что средняя ошибка составляет 0,759151, или 6,58% от среднего значения, что удовлетворительно.

Вывод: степенное уравнение

Расходование = 1,6751· Поступление^0,860959 применимо для описания зависимости между поступлением и расходованием.

д) Гиперболическая функция y = a+ :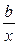

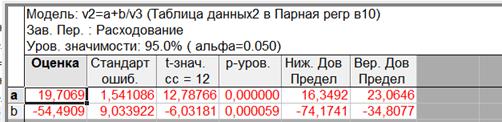
Рис. 1.21– Результаты гиперболической регрессии

Уравнение регрессии: y = 19,7069 –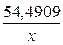

Множитель a значим на уровне α =0,05: p-уровень = 0,00000 < 0,05

Коэффициент b значим: p-уровень = 0,000059 < 0,05

В столбце «Теоретические» зададим формулу =19,7069-54,4909/v1.

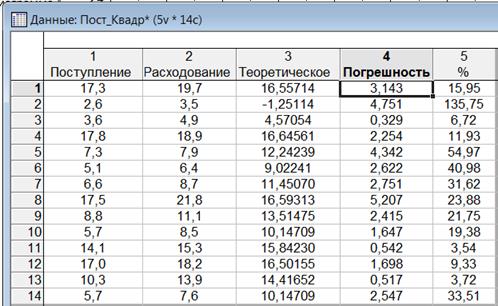
Рис. 1.21 – К вычислению средней ошибки гиперболической регрессии

Далее выполняем команду «Анализ → Описательные статистики и таблицы → Описательные статистики. Определим переменную Погрешность и %. На закладке «Дополнительно» оставим флажок только для среднего значения

Рис. 1.22 – Нахождение средней ошибки гиперболической регрессии

Итак, оценка гиперболическоого уравнения регрессии показывает:

Средняя ошибка составляет 2,48332, или 29,5025% от среднего значения, что вполне приемлемо. Вывод: гиперболическое уравнение

Расходование = 19,7069–54,4909/ Поступление неприменимо для описания зависимости между поступлением и расходованием.