Исходные данные к задаче № 5
| Вариант | 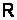 , Ом , Ом
| 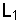 , мГн , мГн
| 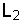 , мГн , мГн
| 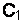 , мкФ , мкФ
| 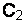 , мкФ , мкФ
| 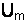 , В , В
| f, Гц |
| – | |||||||
| – | |||||||
| – | |||||||
| – | |||||||
| 0,4 | – | ||||||
| – | |||||||
| – | |||||||
| – | |||||||
| 2,5 | 2,5 | – | |||||
| – | |||||||
| – | |||||||
| – | |||||||
| – | |||||||
| – | |||||||
| – | |||||||
| – | |||||||
| – | 0,5 | ||||||
| – | |||||||
| – | 1,5 | ||||||
| – | |||||||
| – | |||||||
| – | |||||||
| – | 0,5 | ||||||
| – | |||||||
| – |
Ход решения задачи
Переменным током называется электрический ток, изменяющийся с течением времени. Значение электрического тока (эдс, напряжения) в рассматриваемый момент времени называется мгновенным значением тока (эдс, напряжения), а наибольшее (максимальное) значение периодических токов – амплитудой.
В цепи переменного тока, обладающей только активным сопротивлением, ток и напряжение совпадают по фазе, т. е. они одновременно проходят через свои нулевые и максимальные значения. Угол 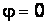 . Действующее значение тока I определяется отношением действующего напряжения U к сопротивлению цепи R:
. Действующее значение тока I определяется отношением действующего напряжения U к сопротивлению цепи R: 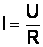 . Мощность цепи
. Мощность цепи 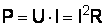 .
.
Расчет цепи ведется так же, как и при постоянном токе.
Всякий потребитель, обладающий индуктивностью, вызывает в цепи переменного тока сдвиг фаз между напряжением и током, причем напряжение опережает ток. Сдвиг фаз между напряжением и током равен 90º.
Сопротивление току, обусловленное действием индуктивности, называется индуктивным, или реактивным, сопротивлением. Обозначается индуктивное сопротивление через 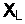 и измеряется в омах (Ом). Величина его определяется по формуле
и измеряется в омах (Ом). Величина его определяется по формуле
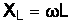 ,
,
где 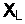 – индуктивное сопротивление; Ом; L – индуктивность, Гн;
– индуктивное сопротивление; Ом; L – индуктивность, Гн; 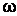 – угловая частота,
– угловая частота, 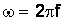 ; f – частота питающей сети, Гц.
; f – частота питающей сети, Гц.
Падение напряжения в индуктивном сопротивлении называется индуктивным падением напряжения и обозначается 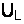 :
: 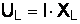 .
.
Из этой формулы следует, что ток 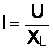 .
.
Переменный ток в цепи с емкостью при отсутствии активного сопротивления и индуктивности опережает напряжение на четверть периода, т. е. сдвинут по фазе в сторону опережения на угол 90°.
Емкостное сопротивление определяется по формуле
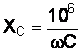 ,
,
где 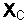 – емкостное сопротивление, Ом; С – емкость, мкФ.
– емкостное сопротивление, Ом; С – емкость, мкФ.
Напряжение на емкостном сопротивлении называется емкостным падением напряжения и обозначается 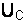 :
: 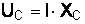 .
.
Из этой формулы следует, что ток 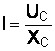 .
.
Полное сопротивление цепи переменного тока, состоящей из активного сопротивления, индуктивности и емкости,
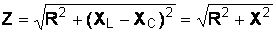 ,
,
где Х – общее реактивное сопротивление, Ом; R – активное сопротивление, Ом.
Действующее значение тока определяется по формуле
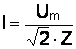 ,
,
где 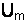 – амплитудное значение напряжения на входе цепи, В.
– амплитудное значение напряжения на входе цепи, В.
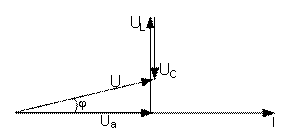
Для построения векторной диаграммы цепи переменного тока, состоящей из активного сопротивления, индуктивности и емкости (рис. 5.1), надо отложить вектор активного падения напряжения 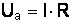 по направлению вектора тока I (рис. 5.2). Вектор индуктивного падения напряжения
по направлению вектора тока I (рис. 5.2). Вектор индуктивного падения напряжения 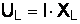 строится под углом 90° к вектору I в сторону опережения, а вектор емкостного падения напряжения
строится под углом 90° к вектору I в сторону опережения, а вектор емкостного падения напряжения 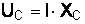 строится также под углом 90° к вектору I, но в сторону отставания.
строится также под углом 90° к вектору I, но в сторону отставания.
Чтобы получить вектор полного напряжения цепи, надо сложить векторы 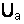 ,
, 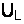 и
и 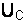 . Угол
. Угол 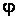 – угол сдвига фаз между током и напряжением на зажимах цепи.
– угол сдвига фаз между током и напряжением на зажимах цепи.

| 
|
| Рис. 5.1. Последовательная цепь переменного тока, состоящая из активного сопротивления, индуктивности и емкости | Рис. 5.2. Векторная диаграмма цепи, изображенной на рис. 5.1 |
Угол сдвига фаз между током и напряжением на зажимах цепи определяется по формулам:
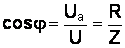 ,
, 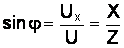 .
.
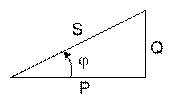
При анализе электрических цепей переменного тока используют треугольник сопротивлений (рис. 5.3), который можно получить из треугольника напряжений, и треугольник мощностей (рис. 5.4), который можно получить, умножив стороны треугольника сопротивлений на квадрат тока.
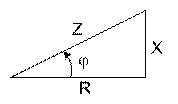
| 
|
| Рис. 5.3. Треугольник сопротивлений | Рис. 5.4. Треугольник мощностей |
В случае равенства индуктивного и емкостного сопротивлений реактивное сопротивление будет равно нулю, а полное сопротивление Zбудет равно активному сопротивлению R. Сдвиг фаз между током и напряжением цепи будет равен нулю ( 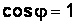 ) и ток в цепи
) и ток в цепи 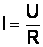 .
.
Этот случай получил название резонанса напряжений. При этом влияние индуктивности и емкости полностью компенсируется, и цепь ведет себя так, как будто она состоит только из активного сопротивления.
При постоянных значениях L и C резонансная частота питающей сети
 .
.
Активная мощность цепи вычисляется по формуле 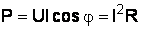 .
.
Реактивная мощность цепи может быть определена через реактивные сопротивления:
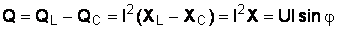 .
.
Полная мощность цепи вычисляется по формуле
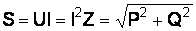 .
.
Единицы мощности для 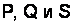 называются по-разному: для
называются по-разному: для  – ватт (Вт), для
– ватт (Вт), для 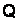 – вольт-ампер реактивный (вар), для
– вольт-ампер реактивный (вар), для  – вольт-ампер (ВА).
– вольт-ампер (ВА).
Задача № 6
РАСЧЕТ ТРЕХФАЗНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
ПРИ СОЕДИНЕНИИ НАГРУЗКИ по схеме «ЗВЕЗДа»
Три потребителя электроэнергии, имеющие одинаковые полные сопротивления фаз 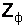 , соединены по схеме «звезда» и включены в четырехпроводную трехфазную сеть с системой симметричных линейных напряжений
, соединены по схеме «звезда» и включены в четырехпроводную трехфазную сеть с системой симметричных линейных напряжений 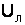 . Определить токи
. Определить токи 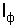 по фазам и в нейтральном проводе
по фазам и в нейтральном проводе 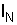 , а также мощность P трехфазной цепи с учетом данных, приведенных в табл. 6.1 для каждого варианта задания. Составить электрическую систему питания. Построить векторную диаграмму напряжений и токов с учетом характера их нагрузки.
, а также мощность P трехфазной цепи с учетом данных, приведенных в табл. 6.1 для каждого варианта задания. Составить электрическую систему питания. Построить векторную диаграмму напряжений и токов с учетом характера их нагрузки.
 2015-05-18
2015-05-18 482
482







