2015-05-20
409
Пусть в некоторой лотерее имеется один выигрыш, размер которого случаен и равен ил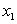и 
, или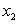 
, …, или 
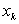. Если лотерея проводится N раз, причем 
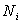раз выпадает выигрыш 
, 
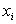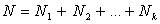, то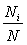 
есть относительная частота выигрыш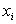а , а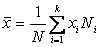 
– средний выигрыш на одну лотерею. Если Х – случайная величина, равная размеру выигрыша в одной лотерее, то из устойчивости относительных частот следует, что 
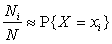. Поэтому средний выигрыш 
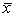колеблется около математического ожидания:
.
Обозначим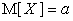 
.
Определение. Центральным моментом s-го порядка случайной величины X называется действительное число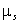 
, определяемое по формуле:
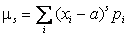, если X – СВДТ;
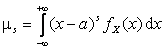, если X – СВНТ.
Замечание. Центральный момент 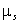существует, если ряд (соответственно интеграл) в правой части каждой из этих формул сходится абсолютно.
Замечание. Иногда используются абсолютные центральные моменты s-го порядка случайной величины X:
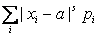, если X – СВДТ;
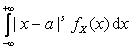, если X – СВНТ;
Определение. Центральный момент второго порядка называется дисперсией случайной величины Х.
|
|
|
Дисперсия случайной величины X обозначается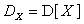 
и выражается через ее закон распределения с помощью формулы:
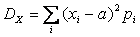, если X – СВДТ;
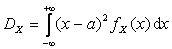, если X – СВНТ.
Определение. Действительное число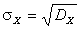 
называется средним квадратическим отклонением случайной величины Х (или иногда стандартным отклонением).
Определение. Случайная величина X называется стандартизованной, есл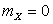и 
и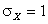 
.
Пример 2.1.16. Закон распределения случайной величины X имеет вид:
| X | –1 | |||
| P | 0,1 | 0,2 | 0,3 | 0,4 |
Вычислить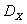 
и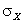 
.
Решение. Найдем вначале математическое ожидание случайной величины X:
.
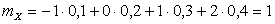Вычислим дисперсию :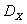
.
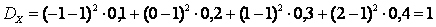Тогда среднее квадратическое отклонение: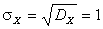 
.
Ответ: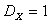 
, 
.
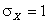Замечание. Можно доказать (Проделайте это самостоятельно!), что для дисперсии верно соотношение:
.
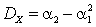С помощью этой формулы вычисление дисперсии обычно (Но не всегда!) упрощается. Так в предыдущем примере при вычислении дисперсии можно было действовать так:
.
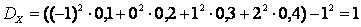Дисперсия случайной величины Х является характеристикой рассеивания. Она характеризует разбросанность случайной величины Х около ее математического ожидания. Дисперсия имеет размерность квадрата случайной величины, что не всегда удобно. Поэтому очень часто используется среднее квадратическое отклонение, которое имеет размерность самой случайной величины.
