Пример 18. 2) A = {f(x1, , xn)| f(1, 1, , 1) = 0} – незамкнутый класс

1) P ₂ – замкнутый класс.

2) A = { f (x ₁,..., x_n)| f (1, 1,..., 1) = 0} – незамкнутый класс.

Возьмем формулу над этим множеством. Пусть f, g ₁,..., g_n Î A, т.е. f (1, 1,..., 1) = 0, g ₁(1, 1,..., 1) = 0, тогда f (g ₁,..., g_n) Î [ A ]. Посмотрим, принадлежит ли функция f (g ₁,..., g_n) множеству А. f (g ₁(1,..., 1), g ₂(1,..., 1),..., g_n (1,..., 1) = f (0,..., 0)), но f (0,..., 0) не обязано быть равным 0.

Пусть, например, g (x ₁, x ₂) = x ₁ Å x ₂, 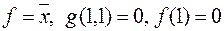, т.е. 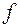и 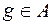. Построим формулу 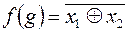, рассмотрим функцию 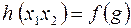на наборе 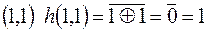, то есть формула не входит в 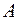и А – незамкнутый класс.

Важнейшие замкнутые классы в Р₂

1) Т₀ – класс функций, сохраняющих константу 0

Т ₀ = { f (x ₁,..., x_n)| f (0,..., 0) = 0}. Покажем, что Т ₀ является собственным подмножеством Р ₂, т.е. Т ₀ ¹ Æ и Т ₀ Ì 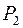(не совпадает с Р ₂). Для этого достаточно привести примеры функций, входящих в Т ₀, и примеры функций из Р₂, не входящих в Т ₀: x ₁& x ₂, x ₁Ú x ₂, x Î Т ₀ и x ₁| x ₂, x ₁ 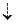x ₂, 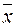Ï Т ₀. Покажем далее, что [ Т ₀] = Т ₀. Вложение Т ₀ Í [ Т ₀] очевидно, так как по определению формулы любая функция из Т ₀ является формулой над Т ₀ и, следовательно, принадлежит [ Т ₀]. Покажем, что [ Т ₀]Í Т ₀. Для этого надо показать, что Ф = f (f ₁,..., f_m) Î Т ₀, если все функции f, f ₁, f ₂, f ₃,..., f _m Î Т ₀. Надо заметить, что в формуле в качестве функции 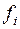могут быть взяты переменные, которые мы договорились считать тождественными функциями. Тождественная функция принадлежит классу Т ₀, поэтому достаточно показать, что если

Ф = f (f ₁,..., f_m) Î [ Т ₀], то Ф(0,..., 0). Действительно,

Ф = f (f ₁(0,..., 0), 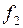(0,..., 0),..., 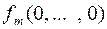) = f (0,..., 0) = 0, так как все функции .

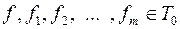Таким образом .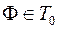

Число функций, зависящих от n переменных и принадлежащих Т ₀, будет равно

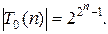
2) T₁ – класс функций, сохраняющих константу 1

T ₁ = { f (x ₁,...) | f (1, 1,...) = 1}; x ₁& x ₂, x ₁Ú x ₂, x Î T ₁, х ₁Å х ₂, x ₁ 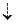x ₂Ï T ₁, следовательно, Т ₁ – собственное подмножество Р ₂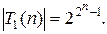

Покажем, что [ T ₁] Í T ₁, обратное включение следует из определения формулы и замыкания. Так как тождественная функция входит в Т ₁, достаточно показать Ф = f (f ₁,..., f_n) Î T ₁, если f, f ₁,..., f_n Î T ₁. Найдем Ф(1,..., 1) = f (f ₁(1,..., 1),..., f_n (1,..., 1)) = f (1,..., 1) = 1, следовательно, Ф = f (f ₁,..., f_n) Î T ₁, отсюда следует [ T ₁] = T ₁.

3) S – класс самодвойственных функций

S = { f (x ₁,...)| f * = f }; x, 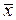, x ₁Å x ₂Å x ₃Î S, x ₁& x ₂, x ₁Ú x ₂, x ₁Å x ₂Ï S,

следовательно, S – собственное подмножество Р ₂. | S (n)| = .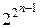

Покажем, что [ S ] Í S. Ф = f (f ₁,..., f_n) Î [ S ], если f, f ₁,..., f_n Î S,

покажем, что Ф Î S. По принципу двойственности,

Ф* = f *(f ₁*,..., f_n *) = f (f ₁,..., f_n) = Ф, отсюда S – замкнутый класс.

4) L – класс линейных функций

L = { f (x ₁,...)| f = c ₀Å c ₁ x ₁Å...Å c_nx_n }; очевидно, L ¹ Æ, с другой стороны L ¹ P ₂, так как x ₁& x ₂ Ï L. Заметим, что тождественная функция принадлежит L и | L (n)| = 2 ^{n +1}. Покажем, что [ L ] Í L. Рассмотрим Ф = f (f ₁,..., f_m), где f, f ₁,..., f_m Î L. Тогда

Ф = а ₀ Å а ₁ (с ₁₀ Å с ₁₁ х ₁ Å...Å c _{1 n}x_{n 1}) Å a ₂(c ₂₀ Å c ₂₁ x ₁ Å

Å c ₂₂ x ₂Å... Å c _{2 n}x_{n 2}) Å...Å a_m (c_{m 0} Å c_{m 1}x₁ Å... Å c_mnx_nm) =

= в ₀ Å в ₁ х ₁ Å...Å в_nх_n, следовательно ФÎ L.

5) М – класс монотонных функций

Определение. Набор 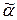= (a₁,..., a_n) предшествует набору 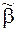= =(b₁,..., b_n) и обозначается 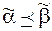, если для 1£i£n a_i£b_i, например: 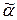= (0010), 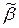= (0110), тогда .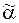

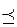
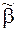Не любые два набора находятся в отношении предшествования, например, наборы (0110) и (1010) в таком отношении не находятся. Отношение предшествования (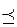) является отношением порядка на множестве наборов длины n. Множество таких наборов будет частично упорядоченным множеством по отношению к операции предшествования.

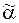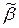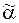
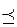
Определение. Функция f(x₁,..., x_n) называется монотонной, если для любых двух наборов и , таких что 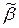, выполняется 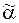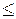f() f(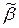). Функции 0, 1, x, x₁&x₂, x₁ Ú x₂ Î M, x₁ Å x₂, x₁~x₂ Ï M.

Для числа монотонных функций, зависящих от n переменных, существуют оценки сверху и снизу, но точное число сосчитать не удается. Покажем, что М – замкнутый класс. Рассмотрим функцию Ф Î[ M ], Ф = f (f ₁,..., f_m), где f, f ₁,..., f_m Î M, причем можем считать, что все они зависят от n переменных. Пусть набор 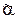= (a ₁,..., a_n),

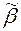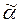
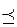
= (b ₁,..., b_n) и 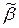. Рассмотрим

Ф(a ₁,..., a_n) = f (f ₁(a ₁,..., a_n), …, f_m (a ₁,..., a_n)),

Ф(b ₁,..., b_n) = f (f ₁(b ₁,..., b_n),..., f_m (b ₁,..., b_n));

,

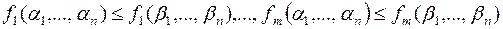тогда набор (f ₁(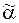),..., f_m (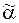)) 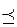(f ₁(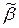),..., f_m (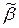)), и так как f Î M, то 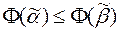, то есть Ф = f (f ₁,..., 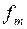) – монотонная функция.

Классы T ₀, T ₁, L, S, M пересекаются, но не совпадают, что видно из табл. 21, где «+» означает, что функция принадлежит данному классу и «-» – не принадлежит.

Таблица 21

	T 0	T 1	L	S	M
x	+	+	+	+	+
	-	-	+	+	-
	+	-	+	-	+
	-	+	+	-	+
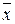
x 1 x 2	+	+	-	-	+