Методы Эйлера

Формой Коши для системы ОДУ является форма, в которой уравнения системы разрешены относительно производных:

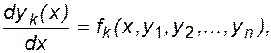(4.7)

где k = 1,2,3,...., n.

Система (4.7) для решения задачи Коши дополняется начальными условиями. В пособии для упрощения выкладок будем решать задачу Коши для одного уравнения:

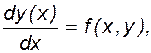
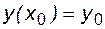. (4.8)

Из теории рядов известно, что любую функцию y(x) в малой окрестности точки х₀ можно разложить в ряд по степеням х, который носит название ряда Тейлора:

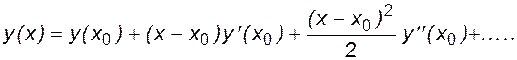(4.9)

Ограничив ряд при малом шаге 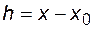двумя членами, получим

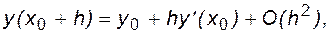(4.10)

где O(h²) - бесконечно малая величина порядка h².

Заменим производную 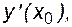входящую в формулу (4.10), на правую часть уравнения (4.8). Отбрасывая бесконечно малую О(h²), получим соотношение, позволяющее найти приближенное решение дифференциального уравнения в точке 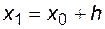, зная значение подынтегральной функции в точке 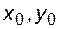, величину производной в данной точке 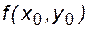и значение шага интегрирования h:

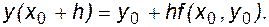(4.11)

Рассчитав значение функции в точке 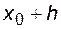, принимаем его за начальное для следующего шага и повторяем расчет. Для любого i- го шага интегрирования будем иметь:

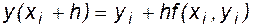или 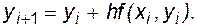(4.12)

Такая формула носит название рекуррентной. Метод численного интегрирования, использующий два члена разложения ряда Тейлора, носит название явного метода Эйлера. Явным этот и другие подобные методы называются потому, что в уравнении используется уже известное значение производной - в точке x_i, то есть производ

ная задается явно. При этом решение находится за конечное, заранее определенное число шагов.

Как известно, уравнение прямой имеет вид y=ax+b, где а - тангенс угла между осью абцисс и прямой, b - значение y при x, равном нулю. Также известно, что геометрический смысл производной - величина производной f’(x) равна тангенсу угла наклона касательной, проведенной к графику кривой функции в данной точке.

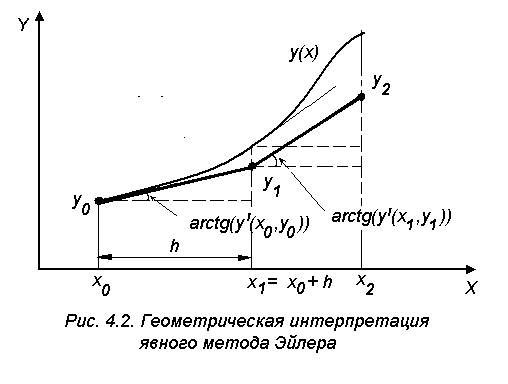
Принимая за аргумент шаг h, можно построить на графике прямую линию из точки x₀,y₀ в точку x₁,y₁ под углом, тангенс которого равен производной в точке x₀ - f(x₀,y₀) (рис.4.2).

Из точки х₁ под углом, тангенс которого равен f(x₁,y₁₎, проводим прямую в точку х₂ и т. д. В качестве решения получим ломаную линию. В связи с этим метод Эйлера еще носит название метода ломаных.

Подставив в формулу (4.12) вместо производной в исходной точке f(x_i,y_i) значение еще неизвестной производной в искомой точке x_i+h - f(x_i+1,y_i+1), получим формулу неявного метода Эйлера:

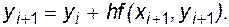(4.13)

Следовательно, неявным называется такой метод, в исходные уравнения которого входят производные еще не рассчитанных точек интегрируемой функции. В общем случае решение уравнений вида (4.13) ищется итерационными методами со свойственными им недостатками (зацикливание, расхождение процесса). Однако, если производную удается представить в линейном виде (линеаризовать)

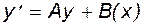, (4.14)

что в задачах электротехники, как правило, имеет место (см. уравнение (1.3) в главе 1 - 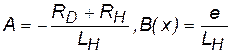), от итерационного метода можно перейти к прямому методу интегрирования неявным методом Эйлера. Подставив выражение для производной из (4.14) в (4.13), получим:

.

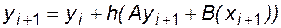Разрешив данное уравнение относительно y_i+1, получим прямую формулу для интегрирования ОДУ неявным методом Эйлера:

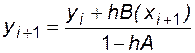. (4.15)

Геометрическая интерпретация неявного метода Эйлера изображена на рис.4.3.

Неявные методы обладают большой устойчивостью при интегрировании жестких ОДУ. Они позволяют проводить интегрирование при больших значениях шага интегрирования h, чем явные методы. Более подробно об этом будет сказано ниже.

На каждом шаге метода Эйлера решение y(x) определяется с погрешностью за счет отбрасывания членов ряда Тейлора, пропорциональных h в степени выше первой. Это означает, что локальная погрешность (погрешность на шаге интегрирования) метода Эйлера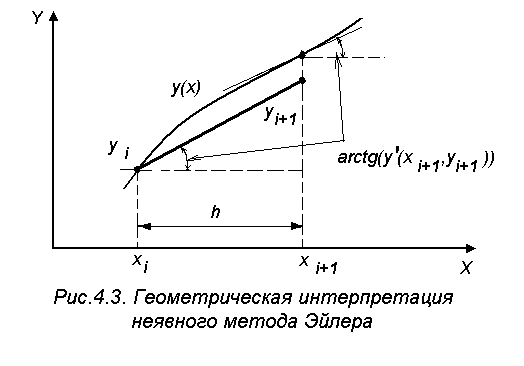
имеет второй порядок. Глобальная погрешность (погрешность на всем интервале интегрирования) имеет первый порядок.

При постоянном шаге h для оценки погрешности применима формула Рунге

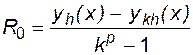, (4.16)

где y_h(x) - приближенное решение ОДУ в точке х, полученное с шагом h; y_kh(x) - приближенное решение того же уравнения, полученное с шагом kh; p - порядок метода.

Процедуры, реализующие явный и неявный методы Эйлера, приведены в конце главы (ПРОГРАММЫ 4.1 и 4.2). Сами процедуры дают решение на шаге интегрирования. Для поиска решения на всем интервале изменения аргумента в вызывающей программе должен быть организовано циклическое изменение аргумента х.

Как видно, метод Эйлера как в явной, так и в неявной форме достаточно просто реализуется на ЭВМ. Коэффициенты А и В неявного метода рассчитываются в вызывающей программе.

Для повышения точности решения разработаны одношаговые методы, позволяющие учесть большее количество членов ряда Тейлора, чем в методе Эйлера. Методов достаточно много [9]. Рассмотрим некоторые из них.