2015-05-20
3028
Имеем таблично заданную функцию - результат натурного или вычислительного эксперимента.
| х | x0 | x1 | x2 | ... | xn |
| f(x) | f0 | f1 | f2 | ... | fn |
Определим аппроксимирующую функцию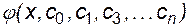 
так, чтобы она совпадала с табличными значениями заданной функции f(x) во всех узлах xi [5]:
; 
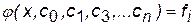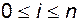. (6.2)
Свободные параметры сi определяются из системы (6.2). Такой способ проведения аппроксимирующей функции называется лагранжевой интерполяцией, а соотношения (6.2) - условиями Лагранжа [1].
Выберем в качестве аппроксимирующей функции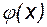 
полином в канонической записи:
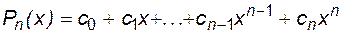. (6.3)
Параметры интерполяции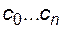 
, которые являются коэффициентами полинома, находятся из условий Лагранжа
, .
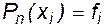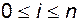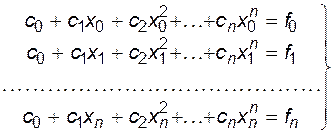. (6.4)
Система линейных алгебраических уравнений (6.4) относительно параметров сi имеет решение, так как определитель системы отличен от нуля, если среди узлов xi нет совпадающих. Определитель системы (6.4) называется определителем Вандермонда и имеет аналитическое выражение [1]. Решив систему (6.4) одним из методов, например, Гаусса, мы получим коэффициенты полинома (6.3). Теперь можно, задаваясь любым значением аргумента х в области значений функции f(x), иметь значение Р(х), близкое к значению f(x).
|
|
|
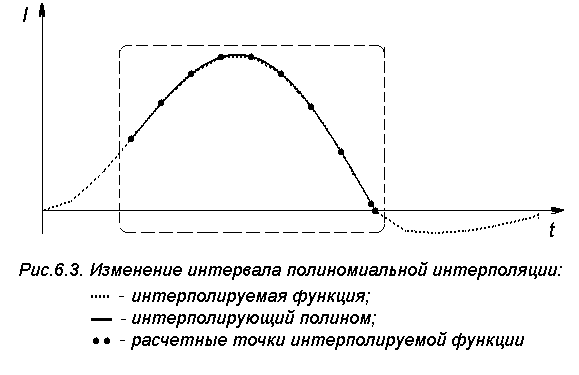
Исследуем вопрос близости f(x) и Р(х), используя результаты расчета тока катушки электромагнита. На рис.6.2 и 6.3 приведены графики интерполируемой функции - тока катушки и результаты полиномиальной интерполяции.
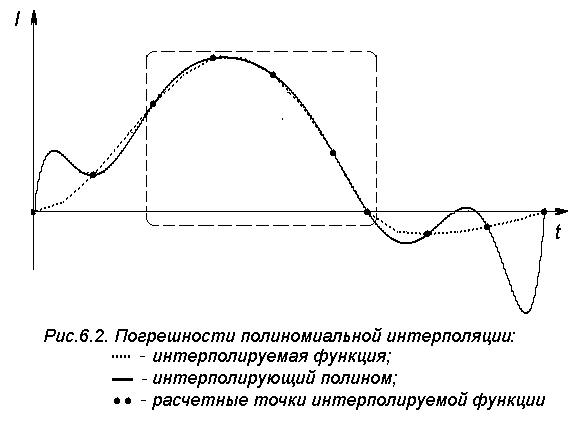
Как видно из рисунков, в обоих случаях использовалось 10 значений интерполируемой функции для поиска коэффициентов полинома. Согласно условиям Лагранжа, значения полинома совпадают со значениями функции в узловых точках. На рис.6.2 видно, что при полиномиальной интерполяции на концах интервала могут возникать существенные погрешности, которые могут полностью исказить результаты расчетов. Заменять полиномом исходную функцию в данном конкретном случае можно лишь в интервале, обозначенном пунктирной линией. Правильно выбранный интервал интерполяции позволяет избежать искажений и повысить точность интерполяции, что иллюстрирует рис.6.3.
Доказано, что интерполяционный полином является единственным [1], то есть любой метод расчета сi в (6.4) дает одинаковый результат, меняется только вычислительный алгоритм.Наиболее известны формы записи интерполяционного полинома, предложенные Лагранжем и Ньютоном. Интерполяционный полином Лагранжа имеет следующий вид:
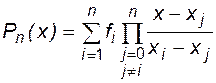. (6.5)
Ньютоном была предложена следующая запись интерполяционного полинома:
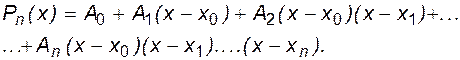(6.6)
А0 = f0, а остальные коэффициенты называются разделенными разностями порядка, соответствующего индексу коэффициента [10].
Погрешность полиномиальной аппроксимации и, в частности, интерполяции определяется соотношением [1]
|
|
|
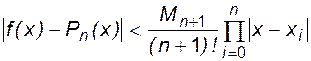, (6.7)
где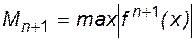 
- максимально возможное по модулю значение n+1 производной аппроксимируемой функции.
Если неизвестны производные функции, то оценку по (6.7) произвести невозможно. При практических расчетах стараются обойти эту трудность, используя различные приемы [1].
Процедура-подпрограмма, формирующая матрицы для расчета коэффициентов полинома методом Гаусса, приведена в конце главы (ПРОГРАММА 6.1).
Расчет коэффициентов Ac[i,j] при параметрах интерполяции сi производится в двух вложенных циклах. При степенях полинома больше 10-12 для получения высокой точности расчетов применение переменных типа REAL становится неприемлемым. В связи с этим, как и в процедуре Canon, так и процедуре Gauss, с помощью которой находятся параметры интерполяции сi, действительные переменные описаны как EXTENDED.
При увеличении числа узлов при полиномиальной интерполяции возникает явление, называемое волнистостью. Это снижает точность полиномиальной интерполяции. Хорошо интерполируются функции, имеющие представление в виде степенных рядов, например, тригонометрические (см. главу 1).
