2. До сих пор Вы использовали линейные алгоритмы, т.е. алгоритмы, в которых все этапы решения задачи выполняются строго последовательно. Сегодня Вы познакомитесь с разветвляющимися алгоритмами.
Определение. Разветвляющимся называется такой алгоритм, в котором выбирается один из нескольких возможных вариантов вычислительного процесса. Каждый подобный путь называется ветвью алгоритма.
Признаком разветвляющегося алгоритма является наличие операций проверки условия. Различают два вида условий - простые и составные.
Простым условием (отношением) называется выражение, составленное из двух арифметических выражений или двух текстовых величин (иначе их еще называют операндами), связанных одним из знаков:
< - меньше, чем...
> - больше, чем...
<= - меньше, чем... или равно
>= - больше, чем... или равно
<> - не равно
= - равно
2.1. Алгоритмы циклической структуры
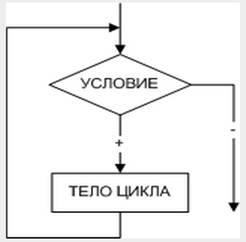
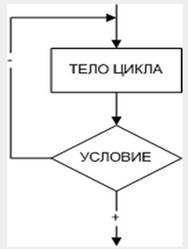
Циклом называют повторение одних и тех же действий (шагов). Последовательность действий, которые повторяются в цикле, называют телом цикла. Существует несколько типов алгоритмов циклической структуры. На рис. 2.1 изображен цикл с предусловием, а на рис. 2.2 - цикл с постусловием, которые называют условными циклическими алгоритмами. Нетрудно заметить, что эти циклы взаимозаменяемы и обладают некоторыми отличиями.
|
|
|
· в цикле с предусловием условие проверяется до тела цикла, в цикле с постусловием - после тела цикла;
· в цикле с постусловием тело цикла выполняется хотя бы один раз, в цикле с предусловием тело цикла может не выполниться ни разу;
· в цикле с предусловием проверяется условие продолжения цикла, в цикле с постусловием - условие выхода из цикла.
| 
|
| Рис. 2.1. Алгоритм циклической структуры с предусловием | Рис. 2.2. Алгоритм циклической структуры с постусловием |
При написании условных циклических алгоритмов следует помнить следующее. Во-первых, чтобы цикл имел шанс когда-нибудь закончиться, содержимое его тела должно обязательно влиять на условие цикла. Во-вторых, условие должно состоять из корректных выражений и значений, определенных еще до первого выполнения тела цикла.
Кроме того, существует так называемый безусловный циклический алгоритм (рис. 2.3), который удобно использовать, если известно, сколько раз необходимо выполнить тело цикла.
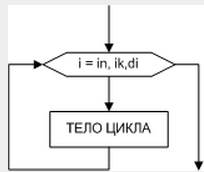
Рис. 2.3. Алгоритм циклической структуры без условия
Выполнение безусловного циклического алгоритма начинается с присвоения переменной i стартового значения in. Затем следует проверка, не превосходит ли переменная i конечное значение iк. Если превосходит, то цикл считается завершенным, и управление передается следующему за телом цикла оператору. В противном случае выполняется тело цикла, и переменная i меняет свое значение в соответствии с указанным шагом di. Далее, снова производится проверка значения переменной i и алгоритм повторяется. Понятно, что безусловный циклический алгоритм можно заменить любым условным.
|
|
|
Отметим, что переменную i называют параметром цикла, так как это переменная, которая изменяется внутри цикла по определенному закону и влияет на его окончание.
Рассмотрим использование алгоритмов циклической структуры на конкретных примерах.
ПРИМЕР 2.1. Найти наибольший общий делитель (НОД) двух натуральных чисел А и В.
Входные данные: А и В.
Выходные данные: А - НОД.
Для решения поставленной задачи воспользуемся алгоритмом Евклида: будем уменьшать каждый раз большее из чисел на величину меньшего до тех пор, пока оба значения не станут равными, так, как показано в таблице 2.1.
Таблица 2.1. Поиск НОД для чисел А=25 и В=15.
| Исходные данные | Первый шаг | Второй шаг | Третий шаг | НОД(А,В)=5 |
| А=25 | А=10 | А=10 | А=5 | |
| В=15 | В=15 | В=5 | В=5 |
В блок-схеме решения задачи, представленной на рис. 2.4, для решения поставленной задачи используется цикл с предусловием, то есть тело цикла повторяется до тех пор, пока А не равно В
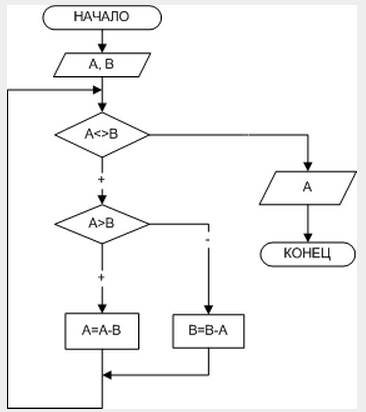
Рис. 2.4. Поиск наибольшего общего делителя двух чисел
ПРИМЕР 2.2. Вычислить факториал числа N (N!=1 2 3 … N).
Входные данные: N- целое число, факториал которого необходимо вычислить.
Выходные данные: factorial- значение факториала числа N, произведение чисел от 1 до N, целое число.
Промежуточные данные: i- целочисленная переменная, принимающая значения от 2 до N с шагом 1, параметр цикла. Блок-схема приведена на рис. 2.5.
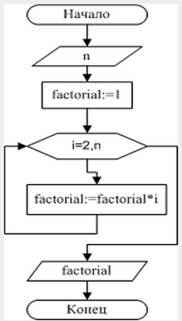
Рис. 2.5. Вычисление факториала
Итак, вводится число N. Переменной factorial, предназначенной для хранения значения произведения последовательности чисел, присваивается начальное значение, равное единице. Затем организуется цикл, параметром которого выступает переменная i. Если значение параметра цикла меньше или равно N, то выполняется оператор тела цикла, в котором из участка памяти с именем factorial считывается предыдущее значение произведения, умножается на текущее значение параметра цикла, а результат снова помещается в участок памяти с именем factorial. Когда параметр i становится больше N, цикл заканчивается, и на печать выводится значение переменой factorial, которая была вычислена в теле цикла.
ПРИМЕР 2.3. Вычислить значения y, соответствующие каждому значению x (xn ≤ x ≤ xk, dx) по формуле:
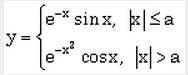
Найти максимальное и минимальное значение у.
Входные данные: xn, xk, dx, a.
Выходные данные: множество значений у, ymax - максимальное значение у, ymin - минимальное значение у.
Алгоритм поиска минимального (максимального) значения переменной у можно описать следующим образом. Пусть минимальное (максимальное) значение y хранится в переменной ymin (ymax). До начала цикла этой переменной присваивается очень большое (маленькое) значение, например, 1020 (-1020). Затем в цикле сравниваются значения y и ymin (ymах), и если встречается значение у меньшее (большее), чем хранится в ymin (ymах), то его необходимо записать в переменную ymin (ymах). Таким образом, все значения у неявно сравниваются между собой, а по окончании цикла в переменной ymin (ymах) будет храниться наименьшее (наибольшее) среди значений у.
.
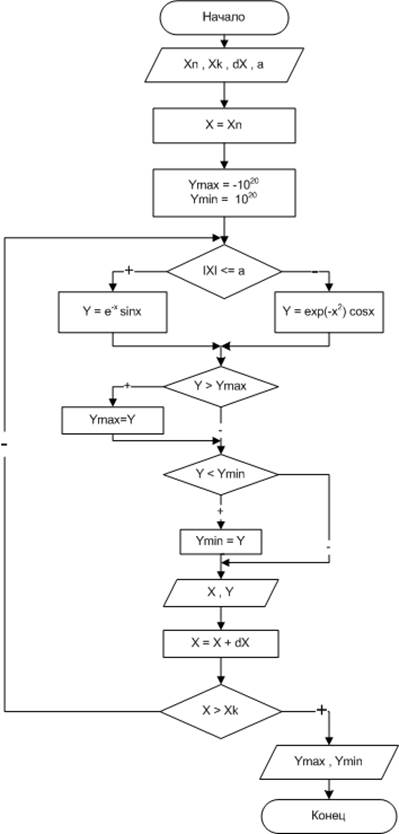
Рис. 2.6. Блок-схема алгоритма примера 2.3
Задание для самостоятельного решения:
Вариант 1.
1. Найти максимальное число из трёх.
2. 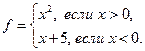
3. Даны три действительных числа. Возвести в квадрат те из них, значения которых неотрицательны, и в четвертую степень — отрицательные.
4. 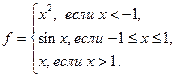
Вариант 2.
1. Найти максимальное число из четырёх.
2. 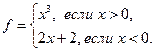
3. Даны два числа. Найти сумму этих чисел, если они положительны, возвести в квадрат оба числа, если они оба отрицательны, и найти модули этих чисел, если хотя бы одно из них отрицательно.
|
|
|
4. 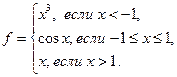
Вариант 3.
1. Найти минимальное число из четырёх.
2. 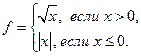
3. Даны два числа. Найти разность этих чисел, если они положительны, возвести в квадрат оба числа, если они оба отрицательны, и найти произведение этих чисел, если хотя бы одно из них отрицательно.
4. 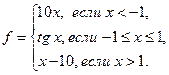
 2015-05-10
2015-05-10 651
651








