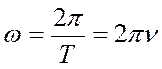Учитывая, что

, (18)

запишем (16) в виде:

у=A cos2π 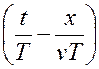(19)

где Т - периодколебания, ν - частота.

Расстояние λ, на которое волна распространяется за период Т

λ=υT (20)

называется длиной волны.

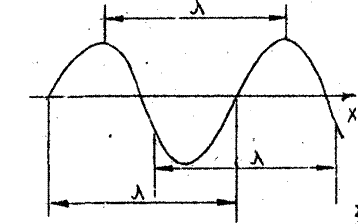
Можно также определить длину волны и как расстояние между двумя ближайшими точками, фазы колебаний которых отличаются на 2π (рисунок 2).

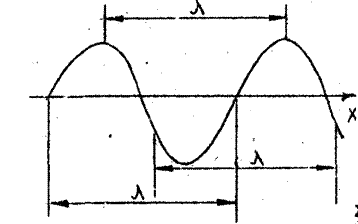Рисунок- 2

В дальнейшем более удобно использовать в уравнении волны косинус. Учитывая (19 и 20), уравнение бегущей волны, распространяющейся в направлении “+x”, можно представить в виде:

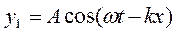(21)

где 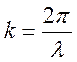- волновое число, показывающее, сколько длин волн укладывается на расстоянии, равном 2π метров.

Для бегущей волны, распространяющейся в направлении “-x”, получим:

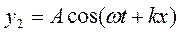(21а)

При распространении бегущей волны происходит перенос энергии в пространстве. Плотность кинетической энергии w_k (равная кинетической энергии единицы объема) составляет

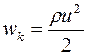, где ρ – плотность среды, u – скорость колебательного движения частиц среды (не путать со скоростью распространения волны v). Поскольку u = dy/dt, то из (21) получим:

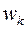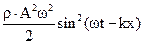= (22)

В отличие от обычных локальных колебаний (математический маятник, груз на пружине и т.п.), потенциальная энергия бегущей волны определяется не смещением некоторого участка от положения равновесия, а его относительной деформацией dy/dx (dx - длина участка в невозмущенном состоянии, dy – изменение длины участка при прохождении волны). Плотность потенциальной энергии (потенциальная энергия единицы объема) равна:

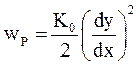(22a)

где K₀ = E.

Дифференцируя (21) по х и подставляя значение v, учитывая (1), получим:

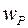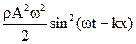= (23)

Примечание 3 Рассмотрим более подробно вывод формулы (23) 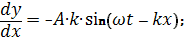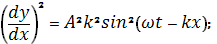Подставляем, найденное значение в выражение (22a). Если K₀ = E, а E = ρ·v², поскольку v = λν, или v = (2π/k)·(ω/2π), E = ω²ρ/k², то

------------------------------------------------

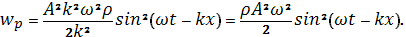
Как видно из (22) и (23), для бегущей волны в любой момент времени выполняется равенство: w_k = w_p. Иначе говоря, кинетическая и потенциальная энергии колеблются в одной фазе (т.е. достигают своих максимальных или минимальных значений одновременно). Это является существенным отличием от локальных колебаний, для которых кинетическая и потенциальная энергии колеблются в противофазе.

Плотность полной колебательной энергии для бегущей волны

w = w_k + w_p.

С учетом (22,23) получим

= =

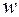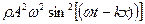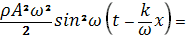
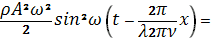
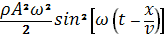= (24).

Эта величина колеблется во времени с частотой, вдвое большей частоты колебаний частиц среды. Среднее по времени значение плотности энергии волны для любой точки, через которую проходит волна, равно

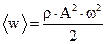(25).

Множитель 0.5 возникает за счет того, что среднее значение квадрата синуса за период как раз равно 0,5.

Таким образом, плотность колебательной энергии, переносимой волной, пропорциональна плотности среды и квадратам частоты и амплитуды.

Особую роль играют гармоническиеволны (см., например, уравнения (16) и (17)). Это связано с тем,что любое распространяющееся колебание, какова бы ни была его форма, всегда можно рассматривать как результат суперпозиции (сложения) гармонических волн с соответственно подобранными частотами, амплитудами и фазами.