Модель парной регрессии. Метод наименьших квадратов

Если теснота взаимосвязи значимая, необходимо построить количественное описание зависимости между экономическими показателями. Количественное описание зависимости между экономическими показателями называется регрессией.

Регрессия строится в виде модели регрессии или уравнения регрессии.

Если исследуется влияние одного экономического показателя x на другой экономический показатель y, то строится модель парной регрессии или уравнение парной регрессии.

Под парной регрессией понимают уравнение зависимости двух переменных: 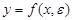, где y – зависимая переменная (результативный признак);

x – независимая, объясняющая переменная (признак-фактор).

В отличие от функциональной зависимости x и y являются реализациями некоторых случайных величин, т. е. регрессию можно понимать как зависимость между случайными величинами. Задача регрессионного анализа – определение зависимости y от х в явном виде. По явному виду зависимости различают линейные и нелинейные регрессии.

Уравнение линейной регрессии имеет вид:

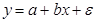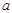, где и 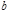- коэффициенты регрессии; 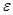- ошибка регрессии (случайная компонента, предназначенная для учета влияния на результирующую переменную y других факторов кроме x).

Коэффициент при независимой переменной b показывает, на сколько единиц в среднем изменится значение независимой переменной y при изменении независимой переменной x на единицу в среднем в принятых единицах измерения.

Коэффициент a не имеет четкой экономической интерпретации, он показывает значение зависимой переменной y при нулевом значении x. Можно интерпретировать знак свободы коэффициента a: если а >0, то относительное изменение зависимой переменной y происходит медленнее, чем относительное изменение независимой переменной x, если a<0, то относительное изменение зависимой переменной y происходит быстрее чем относительное изменение независимой переменной x.

МНК предназначен для оценивания коэффициентов линейной модели парной регрессии. Данный метод основан на предположении о минимизации суммы квадратов отклонений экспериментальных значений результирующей переменной y от ее расчетных значений.

,

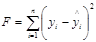Где 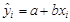- расчетные значения результирующей переменной y.

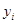- экспериментальное значение.

Необходимым и достаточным условием минимума является

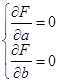
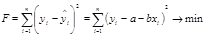
отсюда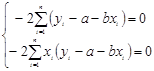

Просуммировав и открыв скобки, получим систему двух уравнений с двумя неизвестными:

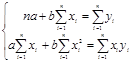
Решая эту систему, получаем оценочные значения коэффициентов регрессии 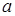и :

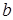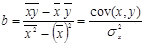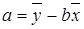; ; где 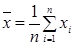; 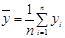- средние выборочные значения исследуемых признаков; 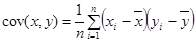- ковариация исследуемых признаков.

Метод, рассмотренный для решения задачи идентификации коэффициентов регрессии, носит название метода наименьших квадратов (МНК). Для того, чтобы полученные оценки коэффициентов регрессии были несмещёнными, состоятельными и эффективными, необходимо соблюдение классических условий (условий Гаусса-Маркова):

1)вид зависимости 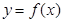- известен;

2)независимые переменные x_i – заданы без ошибок;

-ошибки 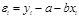подчиняются нормальному закону распределения, причём ;

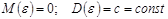3)если независимых переменных x – несколько, то они некоррелированны (это называется отсутствием мультиколлинеарности);

4)последовательные значения ошибок или наблюдений должны быть некоррелированы (отсутствие автокорреляции ошибок или наблюдений).

МНК применим только для идентификации уравнения линейной регрессии. Чтобы использовать данный метод для идентификации уравнений нелинейной регрессии, необходимо линеаризовать уравнение нелинейной регрессии, т. е. путём тождественных математических преобразований привести его к линейному виду.