Звено описывается дифференциальным уравнением второго порядка:
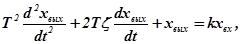 (2.11)
(2.11)
где 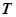 - постоянная времени, характеризующая собственную частоту колебаний системы (звена);
- постоянная времени, характеризующая собственную частоту колебаний системы (звена);
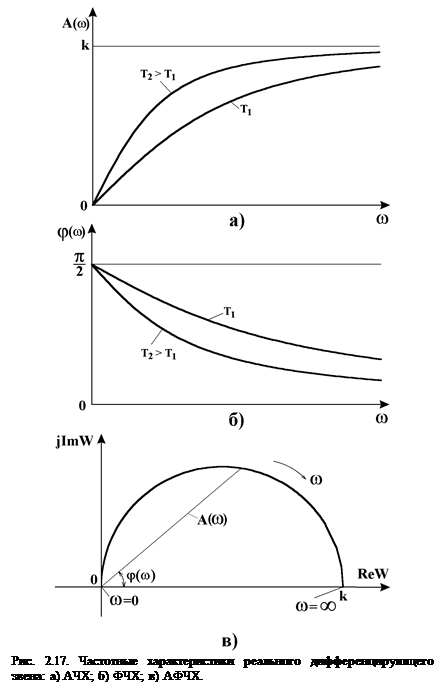 |
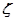 - коэффициент демпфирования;
- коэффициент демпфирования;
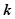 - коэффициент усиления (передачи).
- коэффициент усиления (передачи).
Переходная функция этого звена определяется из решения дифференциального уравнения второго порядка (2.11). Вид переходной функции определяется корнями характеристического уравнения 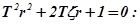
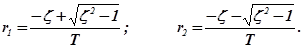
При значениях коэффициента демпфирования 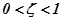 корни будут комплексно-сопряжёнными:
корни будут комплексно-сопряжёнными:

где 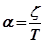 - коэффициент, характеризующий затухание колебаний в ТЗ;
- коэффициент, характеризующий затухание колебаний в ТЗ;
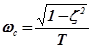 - собственная частота колебаний ТЗ.
- собственная частота колебаний ТЗ.
После решения дифференциального уравнения (2.11) при 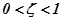 получим переходную функцию колебательного ТЗ:
получим переходную функцию колебательного ТЗ:
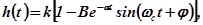 (2.12)
(2.12)
где 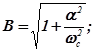
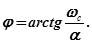
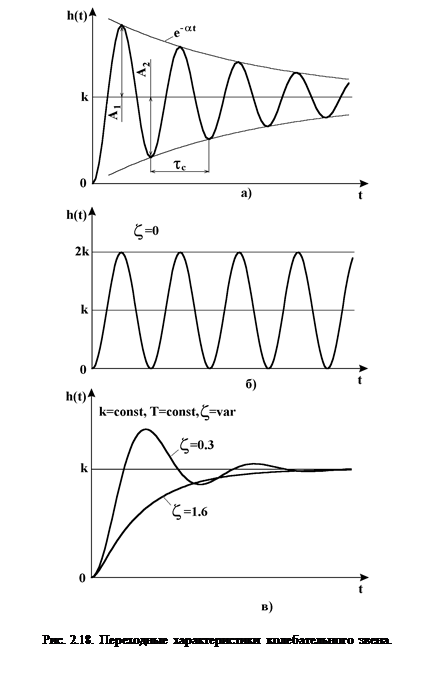
Из анализа переходной характеристики (рис. 2.18,а), построенной по формуле (2.12), следует, что при коэффициенте демпфирования 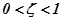 переходный процесс в колебательном ТЗ сопровождается затухающими колебаниями с частотой
переходный процесс в колебательном ТЗ сопровождается затухающими колебаниями с частотой 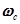 и амплитудой, уменьшающейся по экспоненте
и амплитудой, уменьшающейся по экспоненте 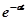 . Промежуток времени между экстремумами, расположенными рядом с одной стороны от нового установившегося значения
. Промежуток времени между экстремумами, расположенными рядом с одной стороны от нового установившегося значения 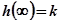 , равен периоду собственных колебаний
, равен периоду собственных колебаний 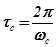 .
.
|
|
|
Если известен переходный процесс для колебательного ТЗ и требуется определить 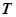 и
и 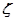 , то достаточно определить
, то достаточно определить 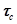 и декремент затухания
и декремент затухания 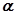 , определяемый по величине снижения амплитуды колебаний за половину периода:
, определяемый по величине снижения амплитуды колебаний за половину периода:
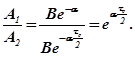 (2.13)
(2.13)
Логарифмируя левую и правую части уравнения (2.13), получим:
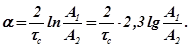
При известных 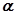 и
и 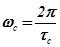 легко определить
легко определить 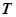 и
и 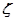 по формулам:
по формулам:
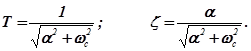
При 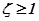 переходная характеристика ТЗ не имеет колебаний и становится похожей на переходную характеристику апериодического ТЗ (рис. 2.18,в). Поэтому колебательное звено при
переходная характеристика ТЗ не имеет колебаний и становится похожей на переходную характеристику апериодического ТЗ (рис. 2.18,в). Поэтому колебательное звено при 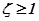 иногда называют апериодическим звеном второго порядка. При отсутствии демпфирования (
иногда называют апериодическим звеном второго порядка. При отсутствии демпфирования (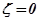 ) колебательное ТЗ называют консервативным колебательным ТЗ. Переходный процесс в этом звене сопровождается незатухающими колебаниями (рис. 2.18,б). На практике всегда имеется трение и потери энергии, поэтому переходный процесс в колебательном ТЗ имеет затухающий характер.
) колебательное ТЗ называют консервативным колебательным ТЗ. Переходный процесс в этом звене сопровождается незатухающими колебаниями (рис. 2.18,б). На практике всегда имеется трение и потери энергии, поэтому переходный процесс в колебательном ТЗ имеет затухающий характер.
Построение переходной характеристики колебательного ТЗ облегчается, если воспользоваться формулой (2.13). Имея в виду, что при 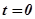 справедливо равенство
справедливо равенство 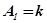 , максимальные отклонения переходной характеристики при
, максимальные отклонения переходной характеристики при 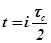 относительно прямой
относительно прямой 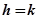 в соответствии с формулой (2.13) будут равны
в соответствии с формулой (2.13) будут равны
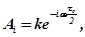
где 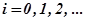 - номер экстремальной точки переходной характеристики.
- номер экстремальной точки переходной характеристики.
Соединяя экстремальные точки плавной кривой, получим переходную характеристику колебательного ТЗ.
Передаточная и частотная функции определяются соотношениями:
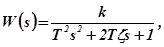
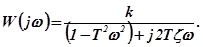 (2.14)
(2.14)
Амплитудная и фазовая частотные характеристики, полученные из выражения (2.14), имеют вид:
|
|
|
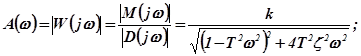
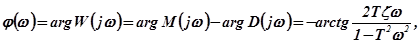 где
где 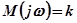 - числитель частотной функции;
- числитель частотной функции;
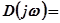
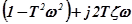 - знаменатель частотной функции.
- знаменатель частотной функции.
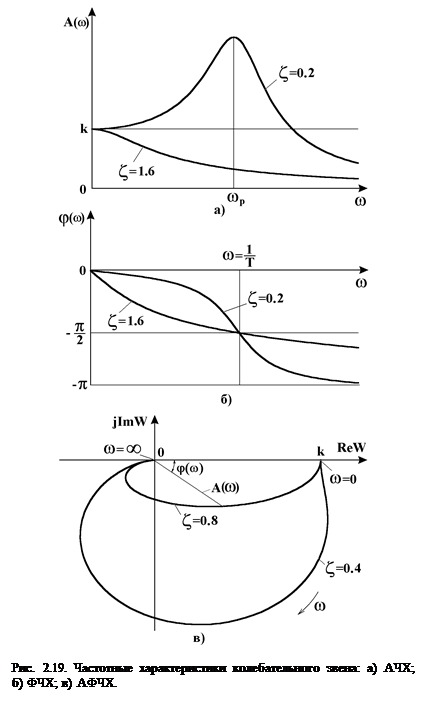
При значениях коэффициента демпфирования 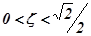 АЧХ колебательного ТЗ представляет собой резонансную кривую (рис. 2.19,а). Резонансная частота колебаний определяется по формуле:
АЧХ колебательного ТЗ представляет собой резонансную кривую (рис. 2.19,а). Резонансная частота колебаний определяется по формуле:
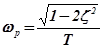 .
.
При 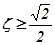 АЧХ колебательного ТЗ представляет собой кривую, похожую на АЧХ апериодического ТЗ. С увеличением частоты колебаний
АЧХ колебательного ТЗ представляет собой кривую, похожую на АЧХ апериодического ТЗ. С увеличением частоты колебаний 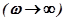 амплитуда колебаний на выходе из колебательного ТЗ стремиться к нулю.
амплитуда колебаний на выходе из колебательного ТЗ стремиться к нулю.
ФЧХ колебательного ТЗ представлена на рис. 2.19,б. Она представляет кривую, асимптотически приближающуюся к значению 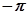 . В консервативном колебательном ТЗ
. В консервативном колебательном ТЗ 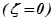 на
на 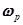 происходит резкая смена фазы выходного сигнала на угол
происходит резкая смена фазы выходного сигнала на угол 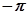 .
.
АФЧХ колебательного ТЗ располагается в IV и III квадрантах комплексной плоскости, как показано на рис. 2.19,в.
 |
 2015-05-13
2015-05-13 897
897







