а) Особой точкой является нижний предел интеграла 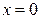 . По определению
. По определению
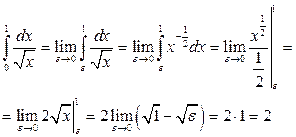 .
.
Интеграл сходится и равен 2.
б) Особой точкой является верхний предел интеграла 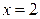 . По определению
. По определению
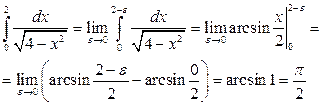 .
.
Учтено, что 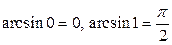 .
.
Интеграл сходится и равен 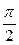 .
.
Заметим: если подынтегральная функция довольно сложная, что затрудняет нахождение первообразной, то для исследования сходимости несобственных интегралов применяют теоремы сравнения, которые позволяют выяснить, сходится или расходится рассматриваемый несобственный интеграл, а также оценить его значение в случае, если он сходится.
3.5. Геометрические и механические приложения определенного интеграла.
- Площадь плоской фигуры.
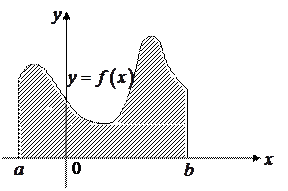 |
Рис.3.10.
Как отмечалось раньше, площадь криволинейной трапеции (рис.3.10.) равна 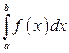 , т.е.
, т.е.
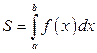 . (3.7)
. (3.7)
Укажем формулы для вычисления площадей плоских фигур, которые не являются криволинейными трапециями.
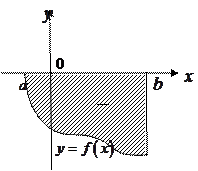 | |||
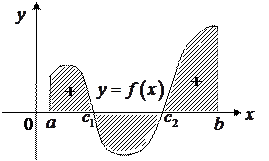 | |||
Рис.3.11. Рис.3.12.
Если 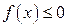 на отрезке
на отрезке 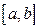 , то определенный интеграл
, то определенный интеграл 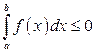 , но его абсолютная величина равна площади фигуры (рис. 3.11.).
, но его абсолютная величина равна площади фигуры (рис. 3.11.).
Поэтому, в этом случае
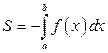 . (3.8)
. (3.8)
Если же функция 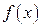 конечное число раз меняет знак на отрезке
конечное число раз меняет знак на отрезке 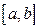 (рис.3.12.), то отрезок
(рис.3.12.), то отрезок 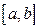 делим на части так, чтобы на каждом частичном интервале функция
делим на части так, чтобы на каждом частичном интервале функция 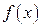 сохраняла знак (см. рис.3.12). Интеграл принимает положительное значение на тех промежутках, где
сохраняла знак (см. рис.3.12). Интеграл принимает положительное значение на тех промежутках, где 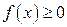 , и отрицательное значение – где
, и отрицательное значение – где 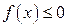 . Для получения площади всей фигуры складываем абсолютные значения всех интегралов по частичным промежуткам. Так, например, для фигуры, изображенной на рис. 3.12, имеем:
. Для получения площади всей фигуры складываем абсолютные значения всех интегралов по частичным промежуткам. Так, например, для фигуры, изображенной на рис. 3.12, имеем:
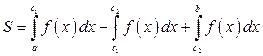 . (3.9)
. (3.9)
Если же область ограничена кривыми 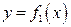 ,
, 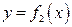 , прямыми
, прямыми 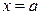 ,
, 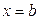 и
и 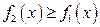 на отрезке
на отрезке 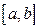 (рис.3.13), то площадь такой области вычисляется по формуле:
(рис.3.13), то площадь такой области вычисляется по формуле:
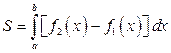 . (3.10)
. (3.10)
Рис.3.13.
► Приведите примеры (графически) плоских фигур, площади которых вычислялись бы соответственно по формулам (3.7)-(3.10).
Если же кривая, ограничивающая область, задана уравнениями в параметрической форме:
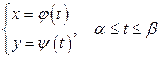 , то для вычисления площади области путем замены переменной в интеграле (3.7) получаем формулу
, то для вычисления площади области путем замены переменной в интеграле (3.7) получаем формулу
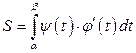 .
.
Для вычисления площади криволинейного сектора (рис.3.14), ограниченного кривой 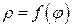 , заданной в полярной системе координат, и радиус – векторами
, заданной в полярной системе координат, и радиус – векторами 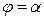 и
и 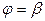 , методом, примененным при получения формулы (3.7) для вычисления площади криволинейной трапеции, получаем следующий результат:
, методом, примененным при получения формулы (3.7) для вычисления площади криволинейной трапеции, получаем следующий результат:
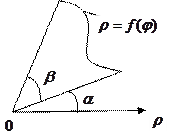
Рис. 3.14
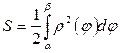
или
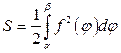 .
.
► Построить кривую 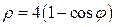 , вычислив значения функции
, вычислив значения функции 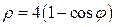 в точках
в точках 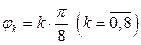 и воспользовавшись четностью функции.
и воспользовавшись четностью функции.
Напомним, что углы считаются отрицательными, если они откладываются от полярной оси по часовой стрелке.
Пример 3.6. Вычислить площадь фигуры, отграниченной линиями 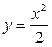 ,
, 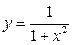 .
.
Решение. Найдем точки пересечения заданных линий. Для этого решим систему уравнений:
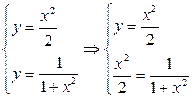 .
.
Решим второе уравнение.
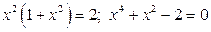 .
.
Получили биквадратное уравнение. Введем новую неизвестную 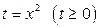 . Для нее получаем квадратное уравнение:
. Для нее получаем квадратное уравнение:
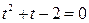 .
.
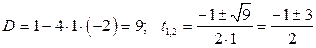 ;
;
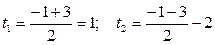 - не рассматриваем, т.к.
- не рассматриваем, т.к. 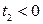 .
.
Отсюда 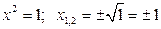 .
. 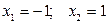 ; соответственно
; соответственно
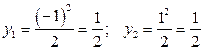 .
.
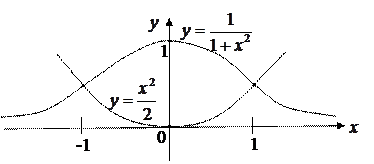 Таким образом, заданные кривые пересекаются в точках
Таким образом, заданные кривые пересекаются в точках 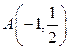 и
и 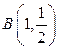 .
.
Рис. 3.15
Для вычисления площади заданной фигуры воспользуемся формулой (3.10).
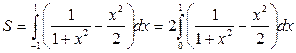 ,
,
т.к. подынтегральная функция четная.
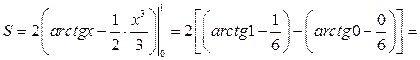
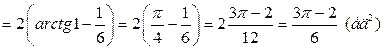 .
.
Напомним, что 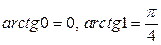 .
.
▶ Найти площадь области, ограниченной линиями:
а) 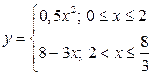 ,
,  (ось
(ось  );
);
б) 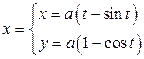 ,
, 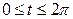 ;
; 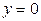 ;
;
в) 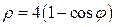 .
.
Ответы: а) 2,0; б) 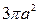 ; в)
; в) 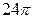 .
.
- Длина дуги кривой.
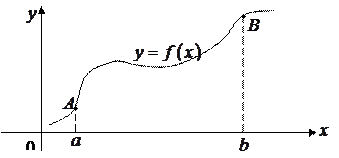 |
Пусть кривая определяется функцией 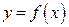 , которая непрерывна и имеет непрерывную производную на отрезке
, которая непрерывна и имеет непрерывную производную на отрезке  . Длина дуги этой кривой, заключенной между такими точками
. Длина дуги этой кривой, заключенной между такими точками 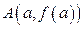 и
и 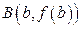 , вычисляется по формуле
, вычисляется по формуле
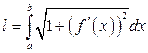 . (3.11)
. (3.11)
Если же уравнение кривой задано в параметрической форме
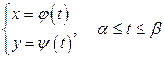 ,
,
функции 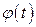 и
и 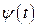 непрерывно дифференцируемы на отрезке
непрерывно дифференцируемы на отрезке 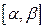 и
и 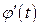 не обращается в нуль на этом отрезке, то длина дуги этой кривой, заключенной между точками, которым отвечает значение параметра соответственно
не обращается в нуль на этом отрезке, то длина дуги этой кривой, заключенной между точками, которым отвечает значение параметра соответственно 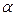 и
и 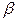 , определяется равенством
, определяется равенством
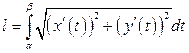 . (3.12)
. (3.12)
Для случая, когда параметрически задается кривая в пространстве
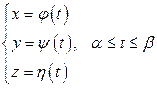 ,
,
длина ее дуги определяется аналогичной (3.12) формулой
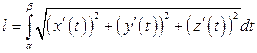 .
.
В ряде случаев кривую удобно рассматривать в полярной системе координат. Пусть ее уравнение имеет вид 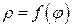 . Тогда длина дуги кривой, заключенной между точками
. Тогда длина дуги кривой, заключенной между точками 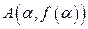 и
и 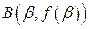 , вычисляется по формуле
, вычисляется по формуле
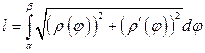 .
.
►Запишите формулы, по которым вы будете вычислять длины дуг кривых.
А) 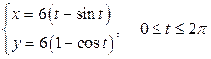 ;
;
б) 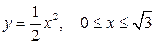 ;
;
в) 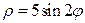 .
.
Пример 3.7. Вычислить длину эллипса 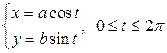 , предполагая, что
, предполагая, что 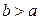 .
.
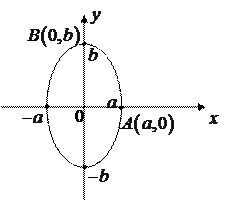 Решение.
Решение.
Вычислим длину дуги 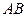 , т.е. длину четверти эллипса, расположенной в первом квадранте. Отметим, что точке
, т.е. длину четверти эллипса, расположенной в первом квадранте. Отметим, что точке 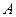 соответствует значение параметра
соответствует значение параметра 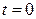 (при этом
(при этом 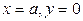 ), а точке
), а точке 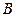 соответствует значение параметра
соответствует значение параметра 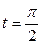 (при этом
(при этом 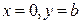 ).
).
Проведем некоторые предварительные вычисления.
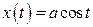 ;
; 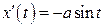 ;
; 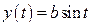 ;
; 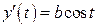 ;
;
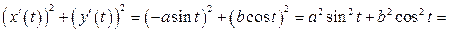
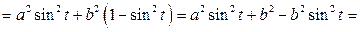
 .
.
Пользуясь формулой (3.12), получим
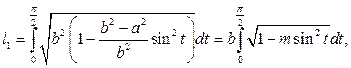
где 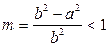 .
.
Длина всего эллипса
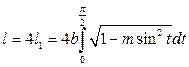 . (3.13)
. (3.13)
Справа в равенстве (13.3) стоит интеграл, который относится к множеству интегралов, не берущихся в элементарных функциях. Он называется эллиптическим интегралом, является функцией от 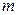 . Значение его при определенном значении
. Значение его при определенном значении 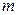 можно найти в таблице [3].
можно найти в таблице [3].
Допустим, 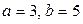 . Тогда
. Тогда 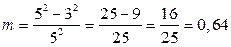 . По таблице при
. По таблице при 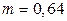 находим
находим 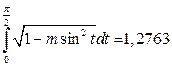 .
.
Тогда 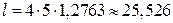 единиц длины.
единиц длины.
Заметим, что мы получили формулу (3.13), пользуясь которой можно найти длину эллипса при любых значениях его полуосей.
Кроме того, отметим, что пользуясь формулой (3.13), мы всегда можем найти длину эллипса, воспользовавшись системой компьютерной математики Mathcad, которая позволяет вычислить определенный интеграл, стоящий справа в равенстве (3.13).
▶ Вычислить длину указанной дуги кривой.
А) 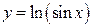 от
от 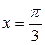 до
до 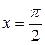 ;
;
б) 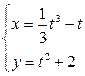 от
от 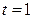 до
до 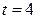 ;
;
в) 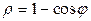 .
.
Ответы: а) 0,549; б) 24,0; в) 8,0.
3) Объем и площадь поверхности тела вращения.
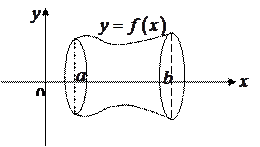 Рассмотрим тело, образованное
Рассмотрим тело, образованное
вращением вокруг
оси  криволинейной
криволинейной
трапеции, ограниченной кривой
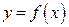 , осью
, осью 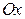 и прямыми
и прямыми
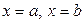 .
.
В этом случае произвольное сечение тела плоскостью, перпендикулярной оси 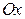 , есть круг, радиуса
, есть круг, радиуса 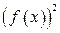 , площадь которого равна
, площадь которого равна 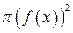 и для объема тела вращения получается формула
и для объема тела вращения получается формула
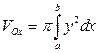 или
или 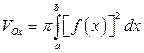 . (3.14)
. (3.14)
Для площади боковой поверхности такого тела вращения получаем формулу
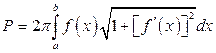 . (3.15)
. (3.15)
Пример 3.8. Вычислить объем и площадь поверхности параболоида, образованного вращением вокруг оси 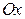 дуги параболы
дуги параболы 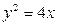 , заключенной между точками
, заключенной между точками 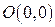 и
и 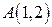 .
.
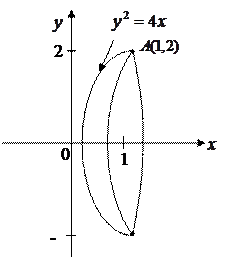 Решение.
Решение.
1) В соответствии с формулой (3.14) объем заданного параболоида равен
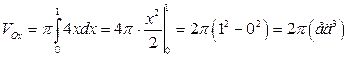 .
.
2) Для вычисления площади поверхности параболоида воспользуемся формулой (3.15).
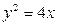 ;
; 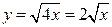 (берем только знак «+», т.к. кривая расположена в первом квадранте).
(берем только знак «+», т.к. кривая расположена в первом квадранте).
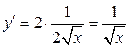 . Следовательно,
. Следовательно,
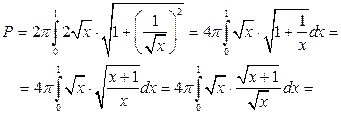
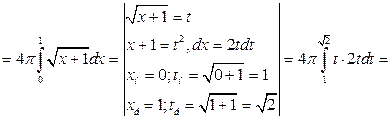
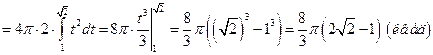 .
.
► Перечислите геометрические приложения определенного интеграла и укажите соответствующие формулы.
► Эллипсоидом вращения (вокруг оси 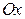 ) называется тело, полученное вращением вокруг оси
) называется тело, полученное вращением вокруг оси 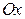 криволинейной трапеции, ограниченной половиной эллипса
криволинейной трапеции, ограниченной половиной эллипса 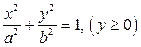 и осью
и осью 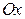 .
.
Найти объем эллипсоида вращения. Сравнить полученную формулу с формулой, по которой вычисляется объем шара.
Ответ: 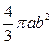 .
.
4. Работа переменной силы
Пусть под действием некоторой силы 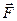 материальная точка движется вдоль оси
материальная точка движется вдоль оси 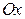 , причем направление силы совпадает с направлением перемещения.
, причем направление силы совпадает с направлением перемещения.
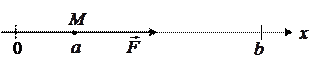 |
Требуется определить работу, произведенную силой 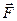 при перемещении точки
при перемещении точки 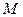 из положения
из положения 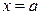 в положение
в положение 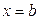 .
.
1) Если модуль силы 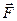 постоянный, т.е. не зависит от положения материальной точки на оси
постоянный, т.е. не зависит от положения материальной точки на оси 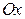 , и равен
, и равен 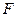 , то работа
, то работа 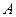 равна произведению модуля силы
равна произведению модуля силы 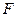 на длину перемещения материальной точки
на длину перемещения материальной точки 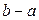 :
:
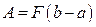 .
.
2) Предположим теперь, что модуль силы  непрерывно меняется в зависимости от положения материальной точки, т.е. является функцией
непрерывно меняется в зависимости от положения материальной точки, т.е. является функцией 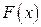 , непрерывной на отрезке
, непрерывной на отрезке 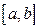 . Тогда работа силы
. Тогда работа силы 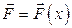 при перемещении материальной точки
при перемещении материальной точки 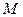 от точки
от точки 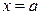 до точки
до точки 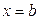 равна
равна
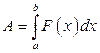 . (3.16)
. (3.16)
Пример 3.9. Известно, что сила  , с которой электрический заряд
, с которой электрический заряд 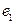 отталкивает заряд
отталкивает заряд 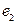 (того же знака), находящийся от него на расстоянии
(того же знака), находящийся от него на расстоянии 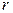 , вычисляется по формуле
, вычисляется по формуле 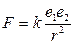 , где
, где 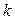 - некоторая постоянная. Определить работу силы
- некоторая постоянная. Определить работу силы 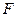 при перемещении заряда
при перемещении заряда 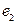 из точки
из точки 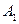 , стоящей от
, стоящей от 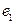 на расстоянии
на расстоянии 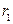 , в точку
, в точку 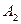 , отстоящую от
, отстоящую от 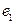 на расстоянии
на расстоянии 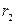 , полагая, что заряд
, полагая, что заряд 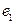 находится в точке
находится в точке 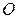 , которая принимается за начало отсчета.
, которая принимается за начало отсчета.
Решение. Поскольку величина силы 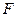 зависит от расстояния
зависит от расстояния 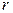 между зарядами, т.е. является переменной
между зарядами, т.е. является переменной 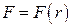 , то вычисляем работу по формуле (3.16)
, то вычисляем работу по формуле (3.16)
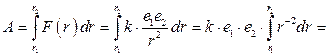
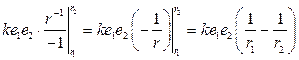 .
.
При 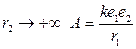 . Если
. Если 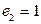 , то при этом
, то при этом 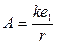 (обозначим
(обозначим 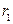 через
через 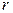 ).
).
Величина 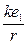 называется потенциалом поля, создаваемого зарядом
называется потенциалом поля, создаваемого зарядом 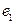 .
.
5. Статистические моменты и координаты центра масс плоской фигуры
Напомним, что статистические моменты материальной точки с массой 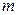 , помещенной в точку
, помещенной в точку 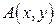 , относительно оси
, относительно оси 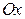 и оси
и оси 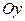 равны соответственно произведениям
равны соответственно произведениям 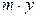 и
и 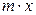 .
.
Рассмотрим материальную плоскую фигуру (пластинку), ограниченную линиями 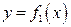 ,
, 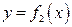 ,
, 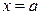 ,
, 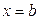 ,
, 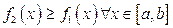 . Поверхностную плотность фигуры, т.е. массу единицы площади поверхности фигуры будем считать постоянной и равной
. Поверхностную плотность фигуры, т.е. массу единицы площади поверхности фигуры будем считать постоянной и равной 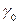 . Такая пластика называется однородной. Тогда масса
. Такая пластика называется однородной. Тогда масса 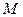 этой пластики вычисляется по формуле
этой пластики вычисляется по формуле
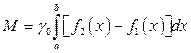 , (3.17)
, (3.17)
а ее статистические моменты относительно осей координат по формулам
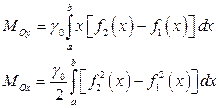 ,. (3.18)
,. (3.18)
Центром масс пластинки называется такая ее точка 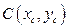 , для которой
, для которой 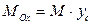 ;
; 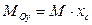 .
.
Отсюда, с учетом равенства (3.17) и (3.18), получаем формулы, по которым вычисляются координаты центра масс однородной пластинки:
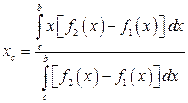 ,
, 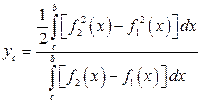 . (3.19)
. (3.19)
► Перечислите механические приложения определенного интеграла и укажите соответствующие формулы.
Пример 3.10. Найти координаты центра масс однородной пластинки, ограниченной линиями 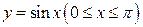 ,
, 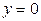 .
.
Решение. Для решения задачи воспользуемся формулами (3.19), в которых положим
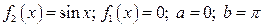 .
.
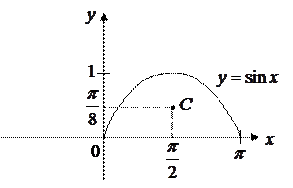 |
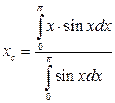 ,
, 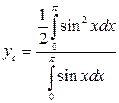 .
.
Вспомогательные вычисления.
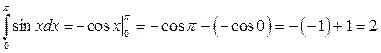 ,
,
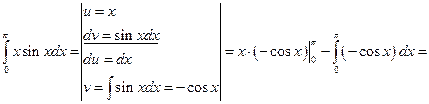
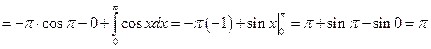 ,
,
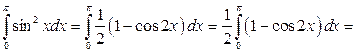
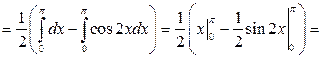
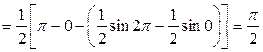 .
.
Используя эти результаты, получим:
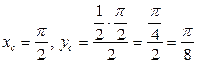 .
.
 2015-05-13
2015-05-13 2256
2256
