Пример 3.2.

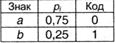
Пусть первичный алфавит состоит из двух знаков а и b с вероятностями, соответственно, 0,75 и 0,25. Сравнить избыточность кода Хаффмана при алфавитном и блочном двухбуквенном кодировании.

При алфавитном кодировании:

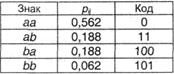
I(А) = 0,811, К(А,2) = 1, Q(A,2) = 0,233

При блочном двухбуквенном кодировании (очевидно, p_ij = p_i ∙ p_j):

I(А) = 1,623 (в пересчете на 1 знак - 0,811), К(А,2) = 1,688 (в пересчете на знак - 0,844), Q(A,2) = 0,040.

Таким образом, блочное кодирование обеспечивает построение более оптимального кода, чем алфавитное. При использовании блоков большей длины (трехбуквенных и более) избыточность стремится к 0 в полном соответствии с первой теоремой Шеннона.

Всякий алгоритм может быть задан посредством тьюринговой функциональной схемы и реализован в соответствующей машине Тьюринга.

Кодирование и обработка в компьютере целых чисел со знаком

Алфавитное неравномерное двоичное кодирование сигналами равной длительности. Префиксные коды

Пример 9.3

Алгоритмическая машина Поста

Вернуться в оглавление: Теоретические основы информатики