Пример 9.4

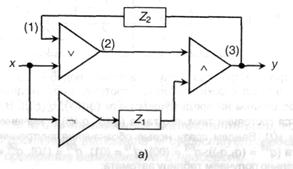
Пусть задана схема (рис. 9.5, а), содержащая по одному логическому элементу И, ИЛИ, НЕ и два элемента задержки (на схеме обозначены Z), на вход которой подается сигнал х. Обозначим внутреннее состояние задержек, соответственно, q₁ и q₂.

Тогда в соответствии со сформулированными выше правилами для выделенных вершин схемы можно записать:

После удаления из исходной схемы задержек перейдем к схеме, представленной на рис. 9.5, б. Она реализует следующие функции:

поэтому канонические уравнения автомата будут иметь вид:

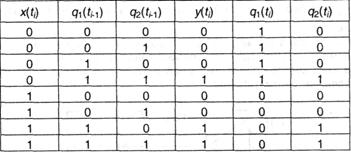
Теперь можно построить представить эти уравнения в виде таблицы значений:

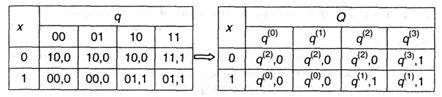
Далее строится таблица команд автомата подобно рассмотренной в примере 9.1. Ее строки и столбцы соответствуют входным символам x(t_i) и состояниям на предыдущем такте (q₁(t_i_-₁), q₂(t_i_-₁)). В клетках размещаются состояния текущего такта (q₁(t_i), q₂(t_i)) и значение выходного символа y(t_i). Введем сразу новые обозначения внутренних состояний автомата (q⁽^p⁾ = (q₁, q₂)): q⁽⁰⁾ = (00), q⁽¹⁾ = (01), q⁽²⁾ = (10), q⁽³⁾ = (11). Тогда окончательно получаем таблицу автомата:

Решение задачи синтеза автомата из логических элементов и элементов задержки производится в обратном порядке: строится система канонических уравнений автомата; автоматные функции представляются в виде таблицы или диаграммы; по ним находится система булевских функций, описывающих работу автомата; по ней - набор логических элементов и связи между ними и, наконец, в них вводятся элементы задержки. Таким образом, теория автоматов позволяет разработать алгоритмические методы перехода от этапа описания характера преобразований, которые должен осуществлять конечный автомат, к конкретным схемным решениям, основанным на использовании рассмотренного выше набора элементов. Это, в свою очередь, дает возможность задачу проектирования новых конечных автоматов формализовать для решения посредством другого конечного автомата, в частности, компьютера. Такая технология действительно существует и широко используется в практике создания новых устройств.