Преобразование сообщений

Вернемся к обсуждению информационных процессов, связанных с преобразованием одних сигналов в другие. Ясно, что технически это осуществимо. Ранее сигналы и их последовательности -сообщения - были названы нами «материальными оболочками для информации», и, естественно, возникает вопрос: при изменении «оболочки» что происходит с его содержимым, т.е. с информацией? Попробуем найти ответ на него.

Поскольку имеются два типа сообщений, между ними, очевидно, возможны четыре варианта преобразований:

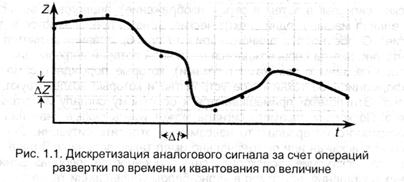
Осуществимы и применяются на практике все четыре вида преобразований. Рассмотрим примеры устройств и ситуаций, связанных с такими преобразованиями, и одновременно попробуем отследить, что при этом происходит с информацией.

Примерами устройств, в которых осуществляется преобразование типа N₁ → N₂, являются микрофон (звук преобразуется в электрические сигналы); магнитофон и видеомагнитофон (чередование областей намагничения ленты превращается в электрические сигналы, которые затем преобразуются в звук и изображение); телекамера (изображение и звук превращаются в электрические сигналы); радио-и телевизионный приемник (радиоволны преобразуются в электрические сигналы, а затем в звук и изображение); аналоговая вычислительная машина (одни электрические сигналы преобразуются в другие). Особенностью данного варианта преобразования является то, что оно всегда сопровождается частичной потерей информации. Потери связаны с помехами (шумами), которые порождает само информационное техническое устройство и которые воздействуют извне. Эти помехи примешиваются к основному сигналу и искажают его. Поскольку параметр сигнала может иметь любые значения (из некоторого интервала), то невозможно отделить ситуации: был ли сигнал искажен или он изначально имел такую величину. В ряде устройств искажение происходит в силу особенностей преобразования в них сообщения, например в черно-белом телевидении теряется цвет изображения; телефон пропускает звук в более узком частотном интервале, чем интервал человеческого голоса; кино- и видеоизображение оказываются плоскими, они утратили объемность.

Теперь обсудим общий подход к преобразованию типа N → D. С математической точки зрения перевод сигнала из аналоговой формы в дискретную означает замену описывающей его непрерывной функции времени Z(t) на некотором отрезке [t₁, t₂] конечным множеством (массивом) {Z_i, t_i} (i - 0...n, где п - количество точек разбиения временного интервала). Подобное преобразование называется дискретизацией непрерывного сигнала и осуществляется посредством двух операций: развертки по времени и квантования по величине сигнала.

Развертка по времени состоит в том, что наблюдение за значением величины Z производится не непрерывно, а лишь в определенные моменты времени с интервалом ∆t:

Квантование по величине - это отображение вещественных значений параметра сигнала в конечное множество чисел, кратных некоторой постоянной величине - шагу квантования (∆Z).

Совместное выполнение обеих операций эквивалентно нанесению масштабной сетки на график Z(t), как показано на рис.1.2. Далее, в качестве пар значений {Z_i, t_i} выбираются узлы сетки, расположенные наиболее близко к Z(t_i). Полученное таким образом множество узлов оказывается дискретным представлением исходной непрерывной функции. Таким образом, любое сообщение, связанное с ходом Z(t), может быть преобразовано в дискретное, т.е. представлено посредством некоторого алфавита.

При такой замене довольно очевидно, что чем меньше п (больше ∆t), тем меньше число узлов, но и точность замены Z(t) значениями Z_i будет меньшей. Другими словами, при дискретизации может происходить потеря части информации, связанной с особенностями функции Z(t). На первый взгляд кажется, что увеличением количества точек п можно улучшить соответствие между получаемым массивом и исходной функцией, однако полностью избежать потерь информации все равно не удастся, поскольку n - величина конечная. Ответом на эти сомнения служит так называемая теорема отсчетов, доказанная в 1933 г. В. А. Котельниковым (по этой причине ее иногда называют его именем), значение которой для решения проблем передачи информации было осознано лишь в 1948 г. после работ К. Шеннона. Теорема, которую примем без доказательства, но результаты будем в дальнейшем использовать, гласит: