СПОСОБ ВРАЩЕНИЯ ВОКРУГ ЛИНИИ УРОВНЯ
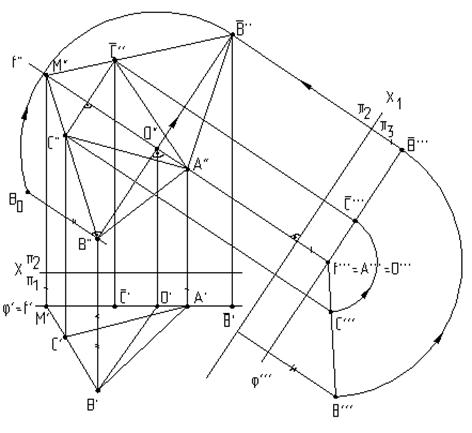
Способ вращения вокруг линий уровня используется в начертательной геометрии главным образом для определения натуральных величин плоских фигур. На рис.6.11 приведен пример определения натуральной величины треугольника АВС. Это решение равносильно решению четвертой основной задачи на преобразование комплексного чертежа и состоит в следующем: Во-первых, в плоскости заданного треугольника проводится линия уровня, например, фронталь, вокруг которой нужно повернуть заданную фигуру до положения, параллельного фронтальной плоскости проекций, или совместить эту фигуру с плоскостью j, проходящей через выбранную линию уровня - фронталь f. Во-вторых, поворот можно осуществить преобразовав заданную плоскую фигуру - треугольник АВС - в проецирующую плоскость, введя дополнительную плоскость проекций p3, перпендикулярную фронтали f. Эта плоскость пересечет плоскость проекций p2 по оси х1. Проецируя треугольник АВС на эту плоскость, получим прямую А”’C”’B”’. Аналогично решению на рис.6.10, плоскость треугольника А”’C”’B”’можно преобразовать в плоскость уровня относительно фронтальной плоскости проекций p2, повернув вокруг фронтали f D А”’C”’B”’до положения Но задача может быть решена без введения дополнительной плоскости проекций p3, так как натуральную величину радиуса вращения точки В можно определить с помощью способа прямоугольного треугольника. Его применение показано на исходном чертеже и дополнительного пояснения не требует.
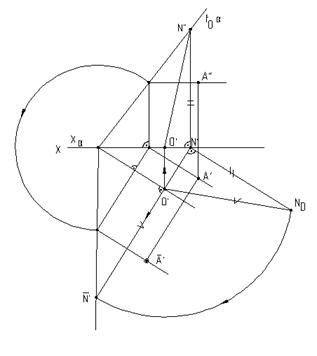
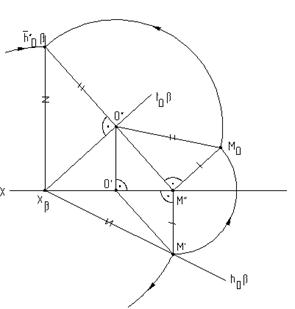
Рис.6.11 В случае задания плоскости ее следами, такую плоскость можно совместить с плоскостью проекций вращением вокруг соответствующего следа этой плоскости. На рис.6.12 плоскость a(h0aÇf0a), заданная следами, совмещена с горизонтальной плоскостью проекций. Для нахождения совмещенного положения плоскости на ее фронтальном следе выбрана произвольная точка N(N``,N`) и из нее опущен перпендикуляр NO(N``O``,N`O`) на горизонтальный след плоскости. Дальнейшее построение аналогично решению задачи на рис.6.11. При совмещении плоскости общего положения с плоскостью проекций может быть найдено совмещенное положение любой фигуры, принадлежащей этой плоскости, например, точки А. На рис.6.13 плоскость b(h0bÇf0b) cовмещена с плоскостью p2. Построения аналогичны и понятны из чертежа. При этом построении точка М(М``,M`) выбрана на горизонтальном следе плоскости, так как совмещение происходит путем вращения плоскости вокруг фронтального следа f0b плоскости b.
Рис. 6.12 Рис.6.13
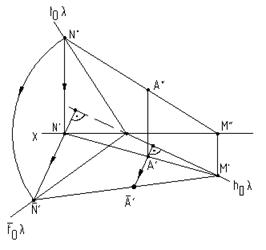
Рис. 5.14 На рис. 6.14 приведен пример совмещения тупоугольной плоскости l с горизонтальной плоскостью проекций. Совмещенное положение Литература: Фролов С.А. Начертательная геометрия. М.: “Машиностроение”, 1983., гл.II, 10,11,12. Гордон В.О. и др. Курс начерт. геом. Изд. “Наука”, М.: Глава V, 34, 37. Локтев В.О. Краткий курс начерт.геом. М.: Гл.VII, 22. |

 ```
``` ```
``` ```. При этом горизонтальная проекция треугольника
```. При этом горизонтальная проекция треугольника