ТЕМА 10. Постоянное гравитационное поле

Сила гравитационного взаимодействия - первая из фундамен­тальных сил, которая была исследована количественно.

В настоящее время можно считать установленным экспериментально, что все тела подвержены гравитационному взаимодействию. Ускорение, которые испытывают различные тела в заданном гравитационном поле, одинаковы – они не зависят от массы и других свойств тел. Сила гравитационного взаимодействия 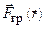зависит от масс взаи­модействующих тел и от расстояния между ними, но явно не зави­сит от скоростей этих тел - только через m (v). Поскольку вcе тела обладают массой (даже, если масса покоя m ₀ = 0), то гравитационное взаи­модействие универсально.

Пусть тела с массами 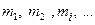создают гра­витационное поле. Рассмотрим действие этого поля на материаль­ный объект массой m, находящийся в точке, к которой проведен радиус-вектор 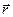. Условимся рассматривать только медленные движения тела: v << c ().

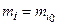Тело массой m называетcя пробным те­лом. Пробное тело мало, т.е.: I) маccа m настолько мала, что своим присутствием пробное тело не нарушает гравитационного поля} 2) протяженность тела массой m мала по сравнению с расстояниями до других тел (вектор 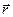имеет смысл радиуса-вектора м.т.). Помещая пробное тело массой m в различные точки пространст-ва, т.е. меняя 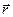, получим всякий раз различные по величине к направлению силы 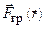. При любом 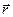сила 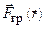пропорциональна m.

Очевидно, что гравитацион­ное воздействие происходит не непосредственно при контакте двух тел (как, например, удар), а на расстоянии (дальнодействие).

Пространство, окружающее тела 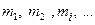, заполнено гравитационным полем. Количест­венной характеристикой воздействия этого поля на материальные объекты следует считать отноше­ние 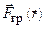к массе пробного тела:

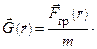(10.1.).

Векторная физическая величина 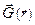, характеризующая состояние гравитационного поля в каждой точке пространства, называется напряженностью гравитацион­ного поля. Вектор напряженности 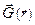определяет силовое действие поля на помещенные в него тела:

Величина 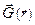не зависит от массы пробных тел. В связи с этим массу пробного тела m называют гравитационным зарядом (по аналогии с электрическим зарядом), а тела 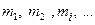- источниками поля.

Необходимо отметить, что понятие массы, введенное ранее как мера инертности тела, и понятие массы как грави­тационного заряда (меры гравитационного взаимодействия) могли бы в принципе быть совершенно различными понятиями. Согласно второму закону Ньютона под действием силы любого происхождения 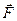тело приобретает ускорение

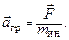(10.2.)

В частном случае гра­витационных сил

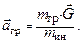(10.3.)

Из опыта известно, что все тела в данном поле 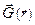обладают одним и тем же ускорением 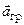= const (у поверхности Земли 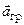= 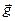). Отсюда можно сделать вывод, что 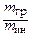=const, т.е. 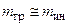. Коэффициент

пропорциональности зависит от выбора системы единиц. В системе СИ 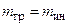(проверка опытами Этвеша и Дикка пока­зала, что равенство справедливо с точностью до 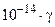). Этот факт назван принципом эквивалентности гравитационной («тяжелой») и инертной масс и лежит в основе построения общей теории относительности.

Итак, 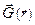- общая характеристика гравитационного поля безотносительно к виду его источников, она определяется экспериментально о помощью пробного тела. Однако важно уметь находить поля, созданные заданным распределением масс, зная поле в самом прос­том случае – поле одной точечной массы.

Закон всемирного тяготения (четвертый закон Ньютона) на ос­нове опытных данных (рис.10.1) сформулирован следующим образом:

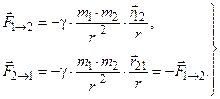, (10.4.)

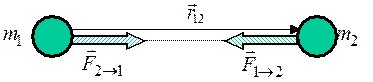где 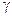- гравитационная постоянная, 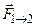- сила притяжения, действующая со стороны массы 1 на массу 2, а 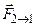- сила притяжения, действующая со стороны массы 2 на массу 1.

Рис.10.1. Гравитационное взаимодействие точечных масс.

Данный закон применим с определенными ограничениями: I) тела 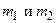покоятся или движутся очень медленно (v << c), 2} тела должны быть материальными точками, т.е. их размеры много меньше расстояния между ними (например, Земля и Луна). Сила 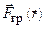- всегда сила притяжения. Формально это следует из того факта, что m > 0; не существует тел c отрицательной массой или нулевой массой (если даже m ₀ =0, то 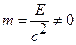, так как 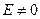). Поэтому под действием только гравитационных сил невозможно равновесие (даже неустойчивое) покоящихся масс. Они имеют тенденцию к стягиванию, например, при очень больших массах сверхплотных звезд происходит гравитационный коллапс.

Гравитационные силы невозможно экранировать (возможность экранирования электрических полей связана с наличием 2-х видов электрических зарядов) – «от гравитационного поля скрыться нельзя».

Гравитационное поле 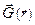точечной массы m - радиальное и сферически симметричное (рис.10.2).

Рис.10.2.Гравитационное поле точечной массы 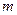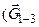- векторы напряженности поля в точках на радиусах 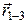, соответственно).

Основная задача расчета гравитационного поля сводится к вычислению его напряженности 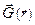при заданном распределении точечных или протяженных масс. Зная 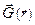, всегда можно найти силу, действующую на пробную массу m.

Как показывает опыт, поле 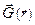, созданное несколькими массами в некоторой точке, есть векторная сумма гравитационных полей отдельных масс :

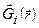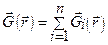(10.5)

Данное утверждение называется принципом суперпозиции и отражает независимость действия полей, отсутствие их влияния друг на друга.

Вектор напряжённости гравитационного поля 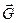точечной массы (рис. 10.3) равен

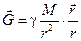. (10.6)

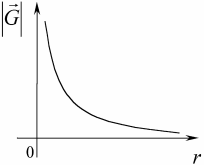
Рис.10.3. Зависимость напряженности гравитационного поля от расстояния.

Размерность напряженности гравитационного поля

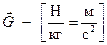
потенциал поля φ – это скрытая энергетическая характеристика поля, которая проявляется при внесении в поле пробного тела (пробной массы или пробного заряда) и зависит от источника поля и от расстояния от него до точки в поле. Потенциал 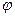– скалярная величина.

Пример расчета потенциала гравитационного поля точечной массы.

На основе взаимосвязи напряженности и потенциала 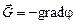получаем:

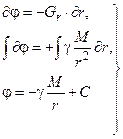(10.7.)

Если считать, что j ® 0 при r ® ¥, тогда С = 0. Следовательно (см. рис. 10.4.),

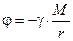(10.8.)

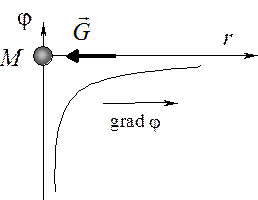Рис. 10.4. Зависимость гравитационного потенциала от расстояния

Скалярной характеристикой взаимодействия в гравитационном поле является потенциальная энергия, величина которой может быть получена на основе взаимосвязи силы и потенциальной энергии:

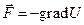(10.9)

Тогда, например, потенциальная энергия взаимодействия (притяжения) двух точечных масс будет равна:

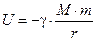(10.10)