2015-05-30
2746
Существует два подхода в минимизации систем булевых функций:
- минимизация каждой функции в отдельности;
- совместная минимизация функций системы.
Рассмотрим первое направление. Если произвести минимизацию булевых функций, входящих в систему, независимо друг от друга, то общая схема будет состоять из изолированных подсхем. Ее можно иногда упростить за счет объединения участков подсхем, реализующих одинаковые члены, входящие в несколько булевых функций системы.
Пусть в результате минимизации функций получены следующие МДНФ:
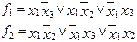
На рис. 2.57 показана реализация системы функций без учета общих частей (термов). Аппаратурные затраты по критерию Квайна без учета инверсий для данной реализации составляют Cb = 18.
На рис. 2.58 показана реализация системы функций с объединением общих частей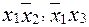 
. Аппаратурные затраты по критерию Квайна без учета инверсий для данной реализации составляют Cb = 14.Очевидно, что данная реализация является более простой (экономичной).
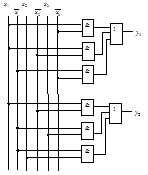
Рисунок 2.57 – Реализация системы функций без учета общих частей
|
|
|
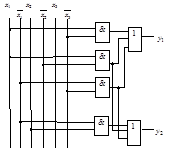
Рисунок 2.58 – Реализация система функций с объединением общих частей
Данный метод не всегда эффективен. Ниже это будет проиллюстрировано примером.
Рассмотрим второе направление. Существуют различные методы, в данном случае предлагается метод минимизации системы булевых функций, являющийся модификацией метода Квайна-Мак-Класки. Алгоритм минимизации следующий. (Для КНФ алгоритм аналогичен).
1. Выписать все минтермы функций (можно в кубической форме), входящие в систему. Каждому минтерму присвоить признак, содержащий номера функций системы, в которые входит рассматриваемый минтерм, например, минтерм 0 (f 1, f 3) 0000, минтерм 15 (f 1) 1111.
2. Выполнить склеивание как в методе Квайна-Мак-Класки. Если признаки склеиваемых элементарных произведений (минтермов и далее импликант) не содержат общих номеров, склеивание не выполняется, поскольку эти элементарные произведения не относятся к одной функции. Результату склеивания (импликантам) присваивать признак, состоящий из номеров функций, общих для двух склеиваемых минтермов или импликант. Не участвовавшие в склеивании импликанты и минтермы являются простыми импликантами и все они составляют сокращенную ДНФ системы, записываемой в виде функции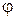 
.
3. Построить таблицу покрытий функции 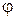, как в методе Квайна-Мак-Класки, с той лишь разницей, что для каждого минтерма выделяется столько столбцов, сколько различных номеров функций содержит его признак. Далее все аналогично, строится минимальная форма функции .
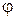4. Произвести получение выражений МДНФ для каждой функции системы по функции .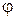
|
|
|
Замечание. Если функция не полностью определена, наборы, на которых она не определена, должны участвовать в склеивании, но в таблицу покрытий не вносятся.
Рассмотрим пример. Пусть дана система булевых функций (табл. 2.8). Найдем МДНФ системы булевых функций.
Таблица 2.8 – Таблица истинности системы булевых функций
| 
|
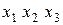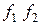| 0 0 0 | 1 1 |
| 0 0 1 | 0 0 |
| 0 1 0 | 0 1 |
| 0 1 1 | 0 1 |
| 1 0 0 | 0 0 |
| 1 0 1 | 1 1 |
| 1 1 0 | 1 0 |
| 1 1 1 | 1 0 |
Выполняем склеивания.
| 0-кубы | 1-кубы | ||
| 0 – 000 (f 1, f 2) | v | 0 (f 1, f 2) È 2 (f 2) = 0х0 (f 2) | |
| 2 – 010 (f 2) | v | 2 (f 2) È 3 (f 2) = 01х (f 2) | |
| 3 – 011 (f 2) | v | 2 (f 2) È6 (f 1) нельзя | |
| 5 – 101 (f 1, f 2) | v | 3 (f 2) È 7 (f 1) нельзя | |
| 6 – 110 (f 1) | v | 5 (f 1, f 2) È 7 (f 1) = 1х1 (f 1) | |
| 7 – 111 (f 1) | v | 6 (f 1) È 7 (f 1) = 11х (f 1) |
В склеивании не участвовали все 1-кубы и два 0-куба 000 (f 1) и 101 (f 2). Это простые импликанты. Они составляют сокращенную ДНФ функции 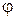. Все они войдут в таблицу покрытий.
Строим таблицу покрытий (табл. 2.9)
Таблица 2.9 – Таблица покрытий
| Простые импликанты | Минтермы функции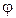 
| ||||||||
| f 1 | f 2 | f 2 | f 2 | f 1 | f 2 | f 1 | f 1 | ||
| A | 0x0 (f 2) | v | v | ||||||
| B | 01x (f 2) | v | v | ||||||
| C | 1x1 (f 1) | v | v | ||||||
| D | 11x (f 1) | v | v | ||||||
| E | 000 (f 1, f 2) | v | v | ||||||
| F | 101 (f 1, f 2) | v | v |
Ядро функции составляют простые импликанты B, D, E, F. Остальные импликанты являются лишними и не будут входить в тупиковую и минимальную ДНФ. Т.е. МДНФ функции 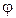будет состоять только из ядра.
МДНФ :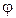
.
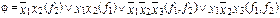По МДНФ функции 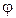строим МДНФ 
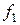и МДНФ 
.
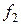МДНФ :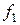 
.
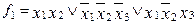МДНФ :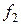 
.
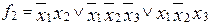Аппаратурные затраты по критерию Квайна без учета инверсий и с учетом объединения общих частей выражения (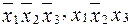
) составляют Cb =16.
Попробуем для минимизации рассмотренной системы воспользоваться первым подходом, предполагающим минимизацию каждой функции отдельно.
Карта Карно для функции 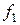представлена на рис. 2.59
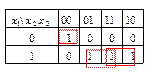
Рисунок 2.59 – Карта Карно для функции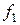
Карта Карно для функции 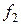представлена на рис. 2.60
МДНФ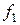
: 
.
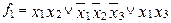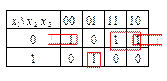
Рисунок 2.60 – Карта Карно для функции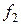
МДНФ :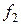 
.
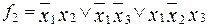Общих частей у МДНФ функций нет, в результате аппаратурные затраты по критерию Квайна без учета инверсий составляют Cb =20. По оценке аппаратурных затрат видно, что раздельная минимизация функций системы уступает совместной, хотя последняя является более трудоемкой.
