Связь дифференцируемости с непрерывностью функции в точке.
Если функция дифференцируема в некоторой точке, то в этой точке функция непрерывна.
Связь диф-ти с сущ-ем производной
Функция дифференцируема в т.х,когда имеет в этой точке конечную производную
8. Дифференциал ф-и в т.х называется число, обозначающееся символом dy и равное
Dy=f’(x)* Δx
Геом. смысл: дифференциал функции у=ƒ(х) в точке х равен приращению ординаты касательной к графику функции в этой точке, когда х получит приращение ∆х.
4. Производной f’(x) функции y=f(x) в т.х наз-ся конечный предел,если он сущ-ет.
Производная - основное понятие дифференциального исчисления, характеризующее скорость изменения функции. Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует
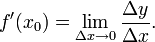
Геометрический смысл: производная 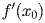 равна тангенсу угла наклона касательной к графику функции
равна тангенсу угла наклона касательной к графику функции 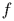 в точке
в точке 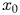 .
.
) Геометрический смысл производной.
Пусть 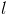 – некоторая кривая,
– некоторая кривая, 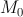 – точка на кривой
– точка на кривой 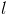 .
.
Любая прямая, пересекающая 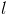 не менее чем в двух точках называется секущей.
не менее чем в двух точках называется секущей.
Касательной к кривой 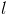 в точке
в точке 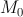 называется предельное положение секущей
называется предельное положение секущей 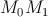 , если точка
, если точка 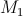 стремится к
стремится к 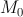 , двигаясь по кривой.
, двигаясь по кривой.
Из определения очевидно, что если касательная к кривой в точке 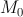 существует, то она единственная
существует, то она единственная
Рассмотрим кривую y = f(x) (т.е. график функции y = f(x)). Пусть в точке 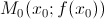 он имеет невертикальную касательную
он имеет невертикальную касательную 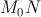 . Ее уравнение:
. Ее уравнение: 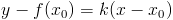 (уравнение прямой, проходящей через точку
(уравнение прямой, проходящей через точку 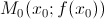 и имеющую угловой коэффициент k).
и имеющую угловой коэффициент k).
По определению углового коэффициента 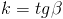 , где
, где 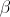 – угол наклона прямой
– угол наклона прямой 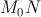 к оси
к оси 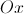 .
.
Пусть 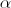 – угол наклона секущей
– угол наклона секущей 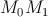 к оси
к оси 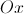 , где
, где 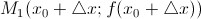 . Так как
. Так как 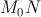 – касательная, то при
– касательная, то при 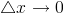
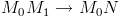 ⇒
⇒ 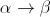 ⇒
⇒ 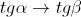 .
.
Следовательно,
.
Таким образом, получили, что 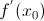 – угловой коэффициент касательной к графику функции y = f(x) в точке
– угловой коэффициент касательной к графику функции y = f(x) в точке 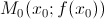 (геометрический смысл производной функции в точке). Поэтому уравнение касательной к кривой y = f(x) в точке
(геометрический смысл производной функции в точке). Поэтому уравнение касательной к кривой y = f(x) в точке 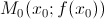 можно записать в виде
можно записать в виде
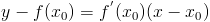
Замечание. Прямая, проходящая через точку 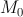 перпендикулярно касательной, проведенной к кривой в точке
перпендикулярно касательной, проведенной к кривой в точке 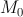 , называется нормалью к кривой в точке
, называется нормалью к кривой в точке 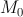 . Так как угловые коэффициенты перпендикулярных прямых связаны соотношением
. Так как угловые коэффициенты перпендикулярных прямых связаны соотношением  , то уравнение нормали к кривой y = f(x) в точке
, то уравнение нормали к кривой y = f(x) в точке 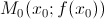 будет иметь вид
будет иметь вид
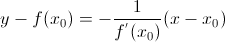 , если
, если 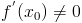 .
.
Если же 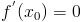 , то касательная к кривой y = f(x) в точке
, то касательная к кривой y = f(x) в точке 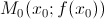 будет иметь вид
будет иметь вид 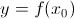 , а
, а
9. Прямая x = a называется вертикальной асимптотой графика функции f (x) при x → a, если выполнено хотя бы одно из условий
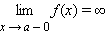 , , 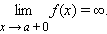
|
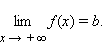 Прямая y = b называется горизонтальной асимптотой графика функции f (x) при x → +∞, если
Прямая y = b называется горизонтальной асимптотой графика функции f (x) при x → +∞, если
Прямая y = kx + b, k ≠ 0 называется наклонной асимптотой графика функции f (x) при x → +∞, если
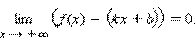
10.Ф-я монотонная на интервале (a,b),если она на этом интервале явл-ся или возрастающей, или убывающей, или невозраст, или неубывающей.
Точки максимума и минимума ф-и называются точками экстремума
.
11. График функции y=f(x) называется выпуклым на интервале (a; b), если он расположен ниже любой своей касательной на этом интервале.
График функции y=f(x) называется вогнутым на интервале (a; b), если он расположен выше любой своей касательной на этом интервале.
Точка, при переходе через которую функция меняет выпуклость на вогнутость или наоборот, называется точкой перегиба. f '' (x 0) = 0.
13. Совокупность всех первообразных функции 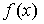 называется неопределенным интегралом от
называется неопределенным интегралом от 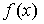 и обозначается
и обозначается 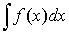 .
.
Св-ва неопределённого интеграла:
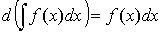
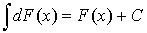
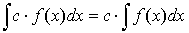
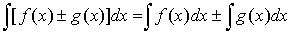
14. Операция нахождения неопределенного интеграла данной функции f(x) на некотором промежутке наз.интегрированием функции f(x).
С помощью таблиц: вычисляемый интеграл окажется один из табличных интегралов,в этом случае для нахождения такого интеграла требуется безошибачно найти соответствующую формулу таблицы и ею воспользоваться.
Метод разложения: интеграл,предложенный для вычисления после применения линейных свойств неопределенного интеграла заменяется линейной комбинацией табличных интегралов.
16. Метод замены переменной (метод подстановки)
Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (то есть подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся. Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой.
Пусть требуется вычислить интеграл 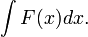 Сделаем подстановку
Сделаем подстановку 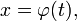 где
где 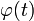 — функция, имеющая непрерывную производную.
— функция, имеющая непрерывную производную.
Тогда 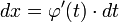 и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой:
и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой:
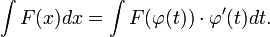
 2015-05-30
2015-05-30 727
727







