Рациональные функции и их интегрирование

Функция 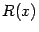называется рациональной функцией, или рациональной дробью, если она представляет собой отношение двух многочленов 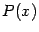и :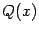

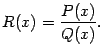
Пусть степень многочле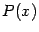на равна 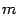, а степень 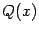равна 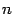, то есть

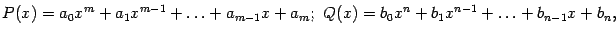
где 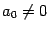и 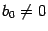. Разделив числитель и знаменатель на число 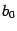, мы получим, что коэффициент при старшей степени 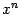в знаменателе равен 1. Для дальнейшего нам будет удобно предполагать, что эта операция уже произведена, то есть что 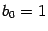. Далее мы будем предполагать, что все коэффициенты 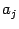и 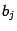-- вещественные числа.

Если 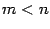, то дробь 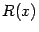называется правильной, а если 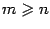, то неправильной. Если дробь неправильная, то её числитель 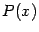можно поделить на знаменатель ,

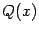получив при этом частное 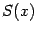и остаток 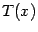, степень которого 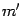меньше 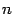. Это означает, что

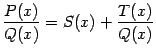
или что

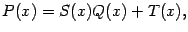
где 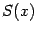-- некоторый многочлен, называемый целой частью рациональной дроби 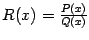. Если остаток 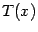тождественно равен 0, то многочлен 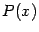делится на 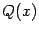без остатка, и функция 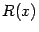является многочленом, то есть совпадает со своей целой частью .

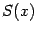С интегрированием целой части дроби 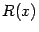, то есть многочлена 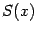, не возникает никаких проблем.

12. Схема исследования функции

1. Область определения

2. Исследование функции на четность, нечетность и периодичность

Если область определения функции симметрична относительно нуля и для любого x из области определения выполнено равенств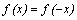о , то 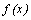– четная функция; если область определения функции симметрична относительно нуля и для любого x из области определения выполнено равенств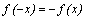о , то 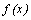– нечетная функция; в противном случае, – общего вида. График четной функции симметричен относительно оси ординат, график нечетной функции симметричен относительно начала координат.

3. Нахождение точек пересечения графика функции с осями координат

Точки пересечения с осью ОХ: 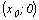, где 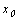– решение уравнения .

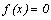Точки пересечения с осью ОY: .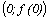

4. Нахождение промежутков знакопостоянства функции

Промежутки знакопостоянства функции – промежутки из области определения функции, где функция принимает положительные или отрицательные значения, т.е. 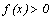или .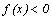

5. Нахождение производной функции, области определения производной, критических точек

Критические точки функции – внутренние точки области определения функции, в которых производная не существует или равна нулю.

6. Нахождение промежутков возрастания, убывания, точек экстремума и экстремумов

Критические точки функции разбивают область определения функции на промежутки. Для нахождения промежутков возрастания, убывания и точек экстремума нужно определить знак производной на каждом из полученных промежутков. Если производная функции положительна на некотором промежутке I, то функция возрастает на этом промежутке; если производная функции отрицательна на некотором промежутке I, то функция убывает на этом промежутке. Если при переходе через критическую точку производная меняет знак, то данная точка является точкой экстремума.

7. Нахождение промежутков выпуклости функции и точек перегиба

Для нахождения промежутков выпуклости используется вторая производная функции. Точки, в которых вторая производная равна нулю или не существует, разбивают область определения функции на промежутки. Если вторая производная на полученном промежутке положительна, то график функции имеет выпуклость вниз, если – отрицательна, то график функции имеет выпуклость вверх. Если при переходе через точку, в которой вторая производная равна нулю или не существует, вторая производная меняет знак, то данная точка является точкой перегиба.

8. Исследование поведения функции на бесконечности и в окрестности точек разрыва

Для исследования поведения функции в окрестности точки разрыва 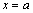необходимо вычислить односторонние пределы: 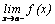и 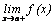. Если хотя бы один из данных пределов равен бесконечности, то говорят, что прямая 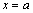– вертикальная асимптота.

При исследовании поведения функции на бесконечности необходимо проверить, не имеет ли график функции наклонных асимптот пр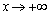и и 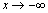. Для этого нужно вычислить следующие пределы: 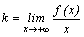и 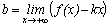. Если оба предела существуют, то 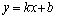– уравнение наклонной асимптоты при 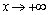. Частный случай наклонной асимптоты при 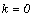– горизонтальная асимптота. Аналогично ищется наклонная асимптота при .

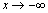9. Построение графика (при необходимости нужно найти значения функции в дополнительных точках)

21. Функции нескольких переменных.

Определение. Если каждой паре (x,y) значений двух независимых друг от друга, переменных величин x и y, из некоторой области их изменения D, соответствует определенное значение величины z, то говорят, что z функция двух независимых переменных x и y, определенная в области D.

22.

Частные производные первого порядка

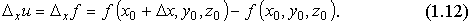Будем рассматривать функции трех независимых переменных. Пусть в некоторой трехмерной области V задана функция u=f(x,y,z) переменных x,y,z и пусть M0(x0,y0,z0) - некоторая внутренняя точка V. Дадим независимому переменному x приращение Δx=x-x0, тогда функция и получит так называемое частное приращение по x: Определение 1.7 Если существует конечный предел отношения частного приращения по x функции f(x,y,z) в точке M0(x0,y0,z0) к вызвавшему его приращению Δx при Δx 0, то этот предел называется частной производной по х функции u=f(x,y,z) в точке М0 и обозначается одним из символов: 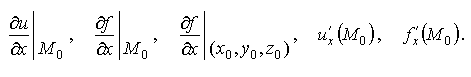По определению, 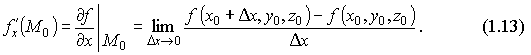Частные производные по y и по z определяются аналогично: 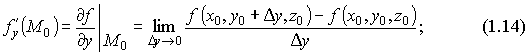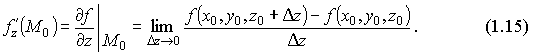Производные f'x, f'y, f'z называются ещё и частными производными первого порядка функции f(x,y,z), или первыми частными производными. Так как частное приращение Δxf(M0) получается лишь за счет приращения независимой переменной x при фиксированных значениях других независимых переменных, то частная производная f'x(M0) может рассматриваться как производная функции f(x,y0,z0) одного переменного x. Следовательно, чтобы найти производную по x, нужно все остальные независимые переменные считать постоянными и вычислять производную по x как от функции одного независимого переменного x. Аналогично вычисляются частные производные по другим независимым переменным. Если частные производные существуют в каждой точке области V, то они будут функциями тех же независимых переменных, что и сама функция. частная производная z'y численно равна тангенсу угла β наклона по отношению к оси Оу, касательной L2 к указанной линии l2 пересечения в точке М(х,у,f(xy)): z'x= tgβ. Предел функции Понятие предела функции является одним из самых важных в математике. Дадим два определения этому понятию. Определение предела по Коши. Число A называется пределом функцииf (x) в точке a, если эта функция определена в некоторой окрестности точки a за исключением, быть может, самой точки a, и для каждого ε > 0 существует δ > 0 такое, что для всех x, удовлетворяющих условию | x – a | < δ, x ≠ a, выполняется неравенство | f (x) – A | < ε. Определение предела по Гейне. Число A называется пределом функцииf (x) в точке a, если эта функция определена в некоторой окрестности точки a за исключением, быть может, самой точки a, и для любой последовательности 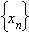такой, что 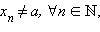сходящейся к числу a, соответствующая последовательность значений функции 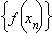сходится к числу A.